Al saber cómo identificar eventos más probables, menos probables o igualmente probables de acuerdo con el número de resultados simples en cada uno de ellos. Podemos identificar más fácilmente cada uno de estos escenarios, tal y como se ha estudiado con anterioridad. 

Es importante recordar que cuando hablamos de resultados simples, nos referimos a aquellos resultados favorables. En estadística se puede definir como todo aquel resultado que se da, de manera indivisible e individual. Por ejemplo, al tirar una moneda y que si resultado sea “corona” o “escudo”. 

En el campo de las finanzas al hablar de los resultados simples, son aquellas utilidades netas. Las cuales se dan de la resta de los gastos totales a los ingresos totales. 

Cuando ya tengamos claros los resultados simples de cada evento se pasaría a definir los criterios claves. Estos criterios se dividen en los resultados más probables, los menos probables y los que son igualmente probables. 

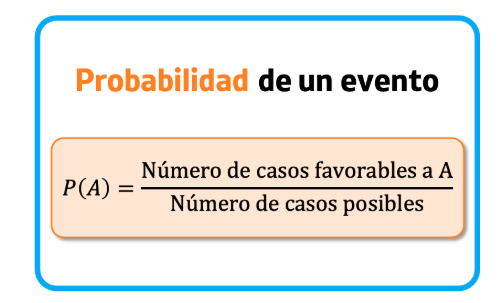
Criterios Claves de los Eventos 

Para poder identificar eventos dentro de las diferentes ramas de la matemática. Es importante tener muy en claro los conceptos de los diferentes resultados que se puede obtener. A continuación, vamos a repasar dichos conceptos, en conjunto con algunos ejemplos. 

• Evento más Probable: Se da cuando se obtienen el mayor número de resultados simples. 

• Evento menos Probable: Se refiere a la probabilidad que obtuvo el menor número de resultados simples. 

• Evento Igualmente Probable: Son todos aquellos resultados simples que igualan a las otras opciones. 

Para entender mejor estos criterios para identificar eventos vamos a dar un ejemplo puntual. 

• Ejemplo: Si contamos un dado con seis caras y lo tiramos en diferentes oportunidades se obtienen los siguientes resultados. 

• Resultado 1: Se da un número par (2, 4, 6), esto se da en 3 resultados distintos. 

• Resultado 2: Se tira el dado y en 3 ocasiones salen números impares (1, 3, 5). 

• Resultados 3: En 1 ocasión se sacó el número 1. 

• Resultado 4: En dos ocasiones se sacó un resultado mayor al número 4 (5 y 6). 

• Ejecución de los Criterios: 

• Evento más probable: Tanto en los resultados 1 y 2, sus eventos son los que cuentan con más probabilidades de suceder. 

• Evento menos probable: El resultado 3, es aquel que posee menor probabilidad de salir. 

• Evento igualmente probable: Tanto los resultados 1 y 2 son igualmente probables para salir. 

Conceptos Clave para Identificar Eventos 

Al definir que los resultados simples son aquellos eventos que se pueden identificar con respecto a su probabilidad (más probable, menos probable e igualmente probable). Dicha comparación se hace a partir de los casos favorables que son aquellos que cumplen con la condición establecidas. 

Sin embargo, también se deben considerar otros conceptos claves que nos ayudaran a identificar eventos de manera clara. Estos son: 

• Espacio Muestral: Se refiere a aquel conjunto de resultados que son posibles. Por ejemplo, al tener un dado, todos los resultados posibles serian 1, 2, 3, 4, 5 y 6. 

• Probabilidad: Es la posibilidad de que un evento pueda o no ocurrir, así mismo como la cantidad de veces que lo pueda hacer. Se expresa generalmente con un 1 (resultado seguro) o con un 0 (resultado imposible). 

• Eventos: Son aquellos subconjuntos de resultados que se pueden dar dentro de un espacio muestral variado. Ejemplo si tenemos un dado se pueden dar resultados impares (1, 3, 5) y resultados pares (2, 4, 6). 

• Experimentos Aleatorios: Referente a todos aquellos resultados que no pueden ser previstos con anterioridad o certeza. 

Importancia de Saber Identificar Eventos 

En matemática, la base para llegar a resultados satisfactorios de un problema se da al poder identificar eventos de una manera correcta y efectiva. Su importancia se da al poder comparar todos los posibles resultados que puede arrojar un evento de acuerdo con sus probabilidades. 

Al conocer todos y cada uno de los posibles resultados, se pueden definir los eventos más probables, los menos probables y los igualmente probables. De esta manera se pueden llevar a cabo la toma de decisiones de una manera más clara, informada y hasta predictiva. Considerando no solo las tendencias, sino también las realidades matemáticas en cada evento.