En la geometría es importante conocer cada una de las características de las distintas figuras geométricas. Pero a la hora de iniciar la resolución de problemas, el calculo del perímetro y área se vuelve información vital para llegar a una solución real y exacta.
Tanto el cálculo del perímetro y área en figuras como los polígonos y el circulo se basan en la suma total de cada uno de los lados para el perímetro. En el caso del área se usan formulas ya establecidas para cada de las figuras geométricas.
Por lo tanto, en el caso de buscar el perímetro de una figura siempre debemos tener presente que solución se da al sumar cada uno de los lados. Esto sin importar la cantidad de lados que posea la figura o su forma, ya que es la totalidad de su contorno que forma la figura geométrica.
El área de una figura se define gracias a las formulas que se utilizan para calcular el espacio que se encuentra en todo el interior de la figura. La fórmula dependerá de cada figura geométrica como por ejemplo en el cuadrado cuya formula es la de base por altura (bxh).
Formulas para el Calculo del Perímetro y Área
Aun cuando las fórmulas más comúnmente utilizadas son las del área, en el perímetro también se dan algunas variaciones dependiendo de la figura que se este utilizando. A continuación, se darán varios ejemplos de cómo lograr el cálculo del perímetro y área, de acuerdo al tipo de figura:
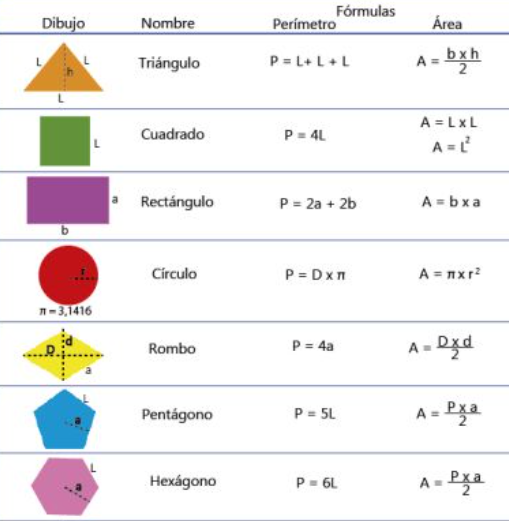
Perímetros
- Circulo: Al tener un contorno redondo no se puede definir propiamente como un lado. Es por esta razón que, para calcular el perímetro de la circunferencia, se hace con una formula distinta.
- P = π . d (Pi por el diámetro).
- P = 2 . π . r (Dos por Pi por el radio).
- Polígonos Regulares: Son aquellas figuras geometrías que poseen todos sus lados con igual medida, de igual forma todos sus ángulos internos son iguales.
- P = n . L (número de lados por la Longitud de los lados).
- Polígonos Irregulares: Se refiere a las figuras en las que al menos uno de sus lados no son iguales a los demás. Por lo tanto, el ángulo interno del lado o los lados distintos, también poseerá una medida diferente a los demás.
- P = L + L + L (Lado más lado más lado), la suma se repite por cada lado que tenga la figura.
- Cuadrado: Al poseer solo 4 lados que son iguales y con ángulos rectos, el cálculo se simplifica.
- P = L+L+ L+L (Lado más lado más lado más lado) o P = 4L (Lado por cuatro).
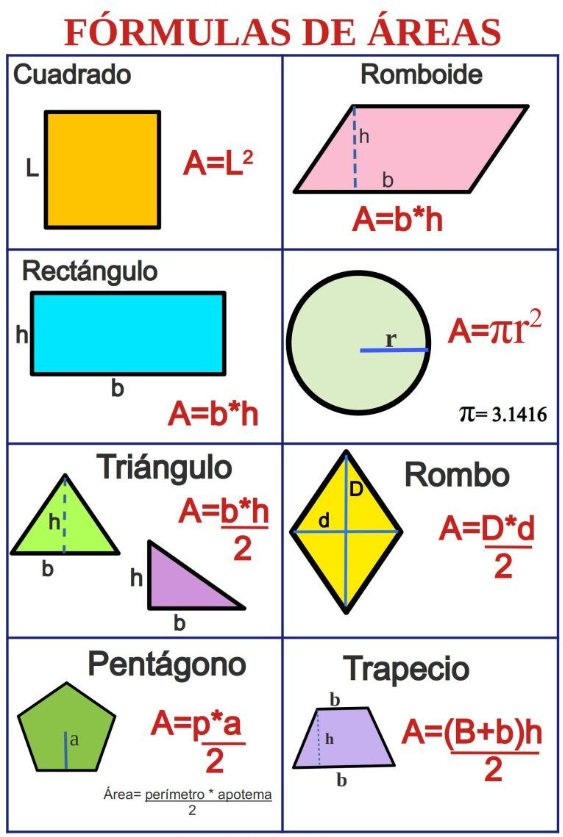
Áreas
- Circulo: Al no poseer lado y en su lugar una circunferencia, se hace uso nuevamente del número π y el valor del radio. El radio se define como la línea recta que va desde cualquier parte del circulo hacia el punto del centro.
- A = π . r² (Pi por el radio al cuadrado).
- Polígonos Regulares: Son aquellas figuras que poseen todos sus lados iguales.
- A = P . Apotema / 2 (Perímetro por la Apotema dividido entre 2).
- Triangulo: Sin importar que tipo de triangulo sea (isósceles, escaleno o equilátero), a la hora de sacar su área se realiza de con la misma fórmula.
- A = b . h / 2 (Base por altura dividido entre 2).
- Rectángulo: Al tener dos lados que son paralelos de mayor medida que la de los otros dos lados, el calculo se hace similar al del cuadrado.
- A = L . h (Largo por ancho).
- Cuadrado: Todos los lados iguales y sus ángulos internos de igual medida.
- A = L² (Lado al cuadrado).
Ejemplo del Calculo del Perímetro y Área
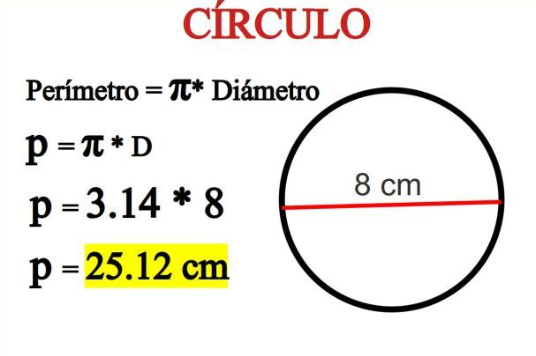
Si tenemos un circulo cuyo radio tiene una medida de 5 cm y un diámetro de 10 cm, se puede indicar los siguiente:
- Perímetro:P = 2 . π . r
- P = 2 . π . 5
- P = 2 . 3,14 . 5 = 31.42 cm.
- Área:A = π . r²
- A = 3,14 . 5²
- A = 3,14 . 25 = 78,54 cm².
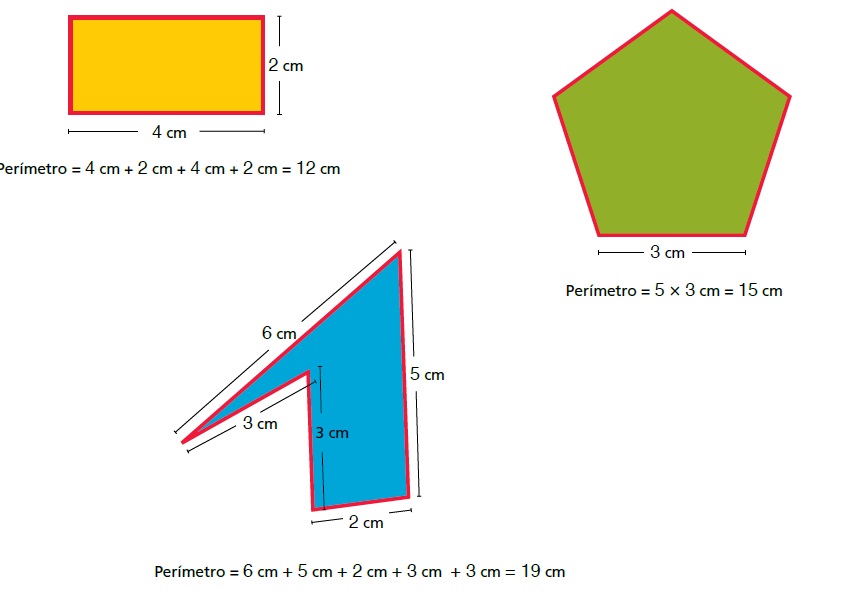
Tenemos una figura poligonal como el Hexágono, cuyo lado mide 10 cm, por lo que el calculo de su perímetro y su área seria de:
- Perímetro:L+L+L+L+L+L (Lado más Lado) o L x 6 (Lado por el número de lados, en este caso 6).
- P = L . 6
- P = 10 . 6 = 60 cm.
- Área:A = P . Apotema / 2.
- A = 60 . 8.66 = 519,6
- A = 519,6 / 2 = 259,8 cm².
Importancia del Calculo del Perímetro y Área
El poder obtener la medida del cálculo del perímetro y área es muy importante en el mundo real, ya que permite cuantificar y medir con exactitud la percepción del espacio. Tanto el conocimiento del perímetro como el área son fundamentales en campos como la construcción, los bienes raíces, la ingeniería, la agricultura, entre muchos otros.
Igualmente, el conocimiento de estos conceptos se vuelven cruciales en diferentes ramas de la matemática como el cálculo, la geometría y el algebra. Esto gracias a que ayuda con el desarrollo de habilidades que incluyen el pensamiento abstracto y lógico en la resolución de problemas académicos y cotidianos.









