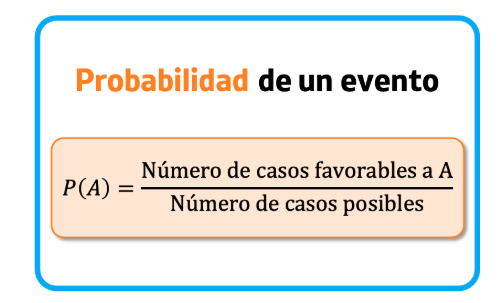
Al estudiar más de cerca sobre el concepto de la probabilidad, es importante que conozcamos la definición clásica o laplaciana de probabilidad. En la cual se establece que la probabilidad que se da en un evento se calcula al dividir el número de casos favorables, entre el número de casos posibles. Siempre y cuando todos los resultados que se den sean igualmente probables.
A esta definición clásica también se le conoce como la formula de Laplace, en honor al francés Pierre-Simón Laplace. El cual vivió entre 1749 a 1827 y fue un renombrado físico, matemático, astrónomo y filosofo. Que siguiendo la mecánica newtoniana pudo descubrir la ecuación Laplace sentando las bases de la teoría analítica de la probabilidad.

La fascinación por el termino de la probabilidad nace del deseo humano por conocer con cierta certeza lo que puede acontecer en el futuro. Esto ya sea para estar preparados y tomar las mejores decisiones o preparase para posibles riesgos.
Según lo dijo el propio Pierre-Simón Laplace “Es notable que una ciencia que comenzó con consideraciones sobre juegos de azar, haya llegado a ser el objeto más importante del conocimiento humano”.
La Fórmula de Laplace
Esta ecuación es muy fácil de llevar a cabo ya que, según su teoría para conocer la probabilidad de un evento, es necesario realizar una división. Al tomar la cantidad de los números de resultados favorables, los cuales representan a los resultados que cumplen con una característica especifica.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en líneaY se divide entre el numero de resultados posibles, los cuales son todos aquellos resultados que pueden darse o ocurrir dentro de un experimento aleatorio. Para sintetizar la probabilidad de un suceso se da al dividir el numero de casos favorables entre el numero de casos posibles dentro de un experimento aleatorio.
Un ejemplo de esta formula se puede dar al lanzar un dado que no este trucado de seis caras al aire y se desea calcular la probabilidad para conseguir un número par.
- Casos Favorables: Existen 3 números que son pares en un dado (2, 4 y 6).
- Casos Posibles: El dado al tener 6 caras, posee 6 posibles resultados en total (1, 2, 3, 4, 5 y 6).
- Probabilidad: Al aplicar la formula de Laplace se obtiene que 3 (números pares) / 6 (posibles resultados) dando como resultado ½ en fracción, 0,5 en decimal o un 50% de probabilidades de salir un número par.
Condiciones para Aplicar la Laplaciana de Probabilidad
Para poder aplicar la definición clásica o laplaciana de probabilidad de manera correcta se debe de cumplir dos condiciones fundamentales, la cuales son:
- Espacio Muestral Finito: Representa al número total de los posibles resultados, los cuales deben ser finitos (presenta un fin).
- Resultados Equiprobables: Esta condición indica que todos y cada uno de los resultados que se den en un experimento deben tener una misma probabilidad de ocurrir. Deben ser igualmente probables, por ejemplo, al lanzar un dada de 6 caras, cada cara posee la misma probabilidad de salir que las demás.

Importancia de la Definición Clásica o Laplaciana de Probabilidad
La importancia de la Laplaciana de Probabilidad radica en sus distintas aplicaciones ya que contribuyo al desarrollo de la teoría de la probabilidad. Algunas de sus más importantes aplicaciones son:
- Histórica: Su definición indica el asentamiento de las bases para el desarrollo de la teoría de la probabilidad.
- Practicidad: En la vida cotidiana y en los experimentos aleatorios funcionan a modo de distracciones o entretenimiento, así como se da o se aplica en los juegos de azar, juegos de lotería o bingos.
- Conexión con Combinatoria: Cuando se dan problemas o experimentos con una mayor complejidad su aplicación se da a través del uso de formulas combinadas. Para incluir los casos favorables y posibles, lo que incrementa su importancia en campos como la estadística o en las finanzas.
- Bases Conceptuales: Ayuda a entender los conceptos más básicos dentro de la probabilidad. Como en el caso de los eventos imposibles en donde P(E)=0 o en los eventos seguros o P(E)=1.

Por tanto, la Laplaciana de Probabilidad se establece como una base fundamental para poder comprender la probabilidad. Estableciendo de esta manera que la probabilidad de un suceso o evento es la razón existente entre los casos favorables y el total de los casos posibles.









