Cuando se habla sobre las relaciones de independencia, desde el punto de vista matemático, se refiere a los casos en donde el valor de un elemento no se ve influido por el valor de otro elemento. Puede aplicarse en distintas áreas de la matemática como la lógica, álgebra lineal, probabilidad, estadística, entre otras.
Su importancia es fundamental ya que a través de ella se pueden comprender las relaciones y estructura de los distintos elementos en cada campo matemático. Es usada para poder simplificar algunos modelos, hacer predicciones y tomar decisiones a partir del análisis de la independencia.
Tipos de Independencia
- Independencia Lógica: En este campo se indica que una sentencia puede ser calificada como independiente. En el caso que no pueda ser probada ni refutada desde los axiomas de una teoría.
- Ejemplos: La hipótesis del continuo (No existe ningún conjunto con cardinalidad, entre los números reales y naturales).
- Independencia Probabilística: Dos eventos pueden ser independientes siempre y cuando el resultado de uno de ellos no afecte la probabilidad del otro.
- Ejemplos: Al lanzar un dado, el resultado de este tiro no afecta el resultado de las tiradas anteriores ni las posteriores.
- Cuando se lanza una moneda en dos ocasiones, dan eventos independientes.
- Independencia Lineal: Usada en el álgebra lineal, en donde los vectores son linealmente independientes, siempre y cuando ninguna pueda ser expresado como una combinación lineal ante las demás.
- Ejemplo: Tres vectores de un espacio tridimensional, si no se encuentran en el mismo plano, pueden ser linealmente independientes.
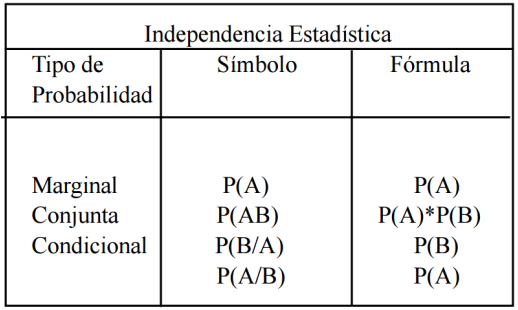
- Independencia Estadística: Indica que dos variables son independientes, en el caso de que el valor de una variable de información sobre el valor de la otra.
- Ejemplo: En el estudio de la relación del color de ojos o del grupo sanguíneo, si no existe la dependencia estadística, el color en los ojos no influye de ninguna manera en el grupo sanguíneo.
- El salario y la altura de una persona pueden ser de manera estadística independientes.
Terminología de las Relaciones Independientes
Otro termino para identificar la independencia es el “indecidible”, el cual puede ser usado en categorías como por ejemplo “sentencia indecidible en la teoría T”. Sin embargo, al usar el termino indecidible puede usar el ámbito de la teoría de computabilidad.
Si hablamos de un problema indecible es aquel cuya respuesta es “si o no” y por tanto no puede ser resuelto por medio de un algoritmo. Estos dos conceptos no son iguales, pero pueden estar relacionados entre sí.
Ejemplos de Independencia
Dentro de la matemática existen muchas sentencias, teoremas, axiomas o enunciados que pueden ser considerados como buenos ejemplos de relaciones de independencia:
- Teoría de Conjuntos de Zermelo-Fraenkel (ZF).
- Teoría de Conjuntos Axiomática.
- Axioma de Elección.
- Hipótesis del continuo.
- Hipótesis del continúo generalizada.
- Teorema de incompletitud de Gödel.
- Aritmética de Peano.
- Sentencia de Gödel.
- Teorema de Goodstein.
- Teorema de Ramsey fuerte.
- Quinto Postulado de Euclides.
- Geometría Euclídea.
- Geometrías no Euclídeas.
Otro claro ejemplo de una relación de independencia es las de la teoría de probabilidades, en la cual se afirma que, si existen dos sucesos aleatorios, estos serán independientes. Esto se da cuando uno de los sucesos no influye sobre el otro suceso, en otras palabras, ambos sucesos no se relacionan.
Uno ejemplo es cuando se tiran los dados en dos ocasiones, por tanto, el resultado de la primera no influye sobre la segunda tirada, ni viceversa. Otro ejemplo de dos sucesos que son independientes es cuando ambos de manera simultanea es igual a la multiplicación de las probabilidades que pase en cada uno. Se puede representar P(AꓵB) = P(A)P(B).
Hay que recordar que en la Independencia es fundamental en las matemáticas para la aplicación y el desarrollo de las mismas. Al no depender de relaciones innecesarias entre los diferentes elementos, permite realizar cálculos, simplificar modelos y construir teorías de manera solida y confiables.
