Se define a una proporción numérica como aquella forma de igualar las razones de una ecuación (c/d = a/b). Es común que para indicar dichas proporciones se utilicen puntos entre las letras o números (a : b :: c : d) . Al querer señalar una ecuación con proporciones directa se puede representar de la siguiente manera (y = kx) indicando que la constante es representada por “K”.
De igual manera se puede representar una proporción numérica por medio de una gráfica en línea recta o por medio de contextos más prácticos como “3 casas para 2 personas”. Todas y cada una de estas representaciones indican que al menos existe una misma relación entre dos pares de números, lo que mantiene una constante de proporcionalidad.
En síntesis, se puede definir a una proporción numérica como una igualdad entre dos cantidades, razones o fracciones. Esto quiere decir que dos cantidades poseen una misma relación como en a/b = c/b. En este caso a es a b como c es a d, lo que ocasiona una multiplicación de extremos (a x d y c x b), lo que ocasiona una codependencia o equivalencia entre las partes.
Propiedades y Componentes
Para tener claro la composición de las proporciones numéricas, se deben tener en claro algunos componentes y sus definiciones.
- Proporción: Se refiere a la igualdad existente en dos razones. Ejemplo a/b = c/d.
- Razón: Cuando se realiza la comparación entre dos cantidades como es el caso de una fracción. Ejemplo: a/b.
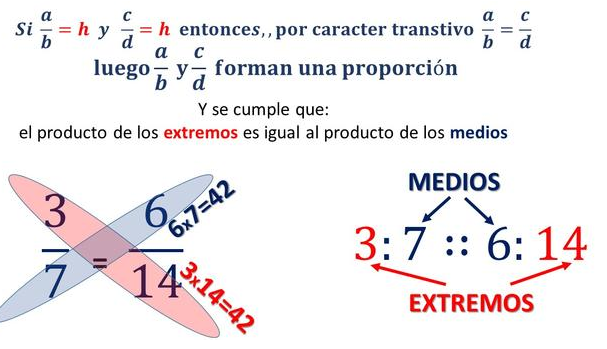
- Medios: Son los números que se encuentran al centro de la comparación. Ejemplo: b y c.
- Extremos: Corresponde a los números que están en los lados externos o extremos de la comparación. Ejemplo: a y d.
- Propiedad Fundamental: Es aquella multiplicación que se realiza entre los extremos y los medios y la cual debe da una igualdad. Ejemplo: a x d = b x c.
Para que nos quede más clara la explicación de cada una de las partes a continuación brindaremos algunos ejemplos.
- Proporción Directa: Si tenemos 2 litros de pintura blanca y estos nos cubren alrededor de 20 mts² (2: 20), por lo tanto 1 litro de pintura roja, nos va a cubrir solo 10 mts², (1:10).
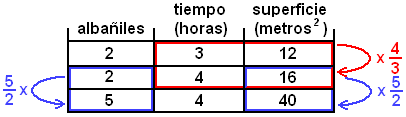
- Proporción Inversa: Si en una construcción 4 trabajadores tardan 10 horas para hacer una pared, eso significa que 8 trabajadores tardaría solamente 5 horas. Ósea a más trabajadores más rapidez de manera proporcional.
- Matemática: Si tengo 2/4 = 3/6, al realizar la multiplicación de los extremos y medios (2 x 6 = 3 x 4) ambos resultados dan 12.
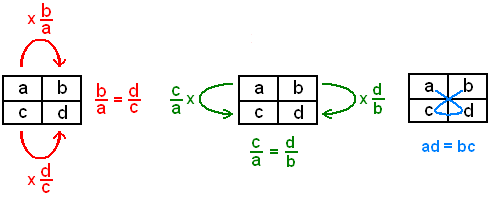
Formas para Representar una Proporción Numérica
Para realizar distintas representaciones de una proporción numérica, se puede hacer de tres maneras las cuales corresponden a la fracción, con símbolo y con ecuación.
- Fracciones: También conocida como de Igualdad de Razones y se refiere a que el cociente o resultado de la división de los números son iguales.
- Ejemplo: 2/5 = 4/10.
2 x 10 = 5 x 4.
20 = 20.
- Símbolos: Relaciona a la Razón y Proporción, en este caso se utilizan los dos puntos para señalar la razón (:) y la proporción es señalada por un doble dos puntos (::).
- Ejemplo: Si tenemos que 2 : 5 :: 4 : 10, lo cual se lee “ dos (2) es a cinco (5), como cuatro (4) es a diez (10)”.
- Ecuación: También se conoce como Proporcionalidad Directa, y se expresa cuando hay una constante dentro de la proporcionalidad. En y = kx, la “k” es la constante, mientras que “y/x” son el valor de la razón.
- Ejemplo: Si en un salón de clases la relación es que por cada 3 niños hay 2 niñas (razón 3/2) y hay 10 niñas en el salón. Para saber cuantos niños hay en total x = 3/2 x 10, por tanto, x = 15 niños.
- Representación Grafica: Se supone que se puede representar una proporción directa dentro de una grafica en forma de una línea recta (0, 0).
Importancia de la Representación de una Proporción Numérica
La representación de una proporción numérica es fundamental para poder resolver y entender algunos problemas científicos y cotidianos. Ya que esta relación nos permite comparar y mantener relaciones constantes entre las diferentes cantidades.
Al cocinar y ajustar las recetas o para saber como dosificar los medicamentos o en la arquitectura al señalara la escala en los planos. La proporción numérica se ha vuelto muy versátil y útil en la vida cotidiana.









