En matemáticas cuando se desean expresar valores de unidades en cantidades muy grandes, estas se pueden expresar por medio de los múltiplos. En términos sencillos, cada unidad de medida posee una unidad base para especificar sus medidas, como el gramo para la masa o el metro para la distancia.
Cuando se deban expresar cantidades numéricas mayores a las de la unidad base. Se usan los múltiplos, lo cuales se obtienen al multiplicar la unidad base por factores de 10. Por lo general los tres primeros después de la unidad base son los mas reconocidos y utilizados en la cotidianidad.
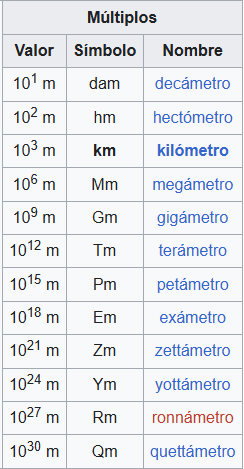
Prefijos y Factores
Para poder identificar cada uno de los múltiplos por encima de las unidades básicas se utilizan prefijos y símbolos, según el factor utilizado. Sin importar cual sea la unidad base (metros/distancia, metro cubico/ volumen, gramo/masa, entre otras), los múltiplos estarán en el mismo orden y bajo el mismo prefijo.
- Deca-: Utiliza el símbolo da y su valor es de 101.
- Hecto-: Con el símbolo h, con un factor de 102.
- Kilo-: Usa el símbolo de k y utiliza el valor de 103.
- Mega-: Con el símbolo de M y su factor es el de 106.
- Giga-: Su símbolo es G, su valor es de 109.
- Tera-: Utiliza como símbolo la T, usa el valor de 1012.
- Peta-: Con símbolo P, usa el factor de 1015.
- Exa-: Tiene como símbolo la E, con el valor del factor 1018.
- Zettá-: Usa como símbolo la Z y usa el factor 1021.
- Yottá-: Su símbolo es la Y, con el valor de 1024.
- Ronná-: Utiliza el símbolo de R y su valor es de 1027.
- Quettá-: Posee el símbolo Q, con un factor de 1030.
Conversiones entre los Múltiplos y los Submúltiplos
Al existir los múltiplos, que son los que expresan cantidades mayores a la unidad base, también existen los submúltiplos que indican las cantidades menores a dicha unidad. Para representar a estas unidades se puede utilizar una escalera. En donde cada escalón representa a un múltiplo o submúltiplo y estando la unidad base en el centro.
Si se necesitara convertir cantidades de un múltiplo a un submúltiplo o viceversa se debe utilizar la división o la multiplicación para ello. Siguiendo con la idea de una escalera, los múltiplos se ubicaría al subir los escalones, mientras que si se bajan estaríamos yendo a los submúltiplos.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en líneaTomando este punto de partida, si necesitamos subir las escaleras o pasar de un múltiplo a un submúltiplo, se multiplica por la potencia de 10 que corresponde. Por otra parte, si la cantidad va a pasar de submúltiplos a múltiplos, se debe dividir por la potencia de 10.
Los Múltiplos de la Unidad de Volumen
Según el SI (Sistema Internacional de Medidas), la unidad de medida para el volumen corresponde al metro cubico (m³). Si tomamos esto como base podremos definir sus múltiplos de la siguiente manera:
- Metro Cubico (m³): Es considerada la unidad básica del volumen. Estaría posicionada en el centro de la escalera de conversiones.
- Decámetro cubico (dam³): Ubicado un escalón por encima de la unidad básica y equivale a 1000 m³ (1dam³ = 1000m³).
- Hectómetro cubico (hm³): Se encuentra dos escalones por encima de la unidad base y su equivalencia es de 1,000,000 de m³ (1hm³= 1000000 m³).
- Kilometro cubico (km³): Esta en el tercer escalón por encima de la unidad base y su valor corresponde a 1,000,000,000 m³ (1km³= 1 000 000 000 m³).
Las Reglas para la Conversión
- Se debe tener claro cual es la unidad base con la que se va a trabajar y convertir (gramos, metros, litros, entre otras).
- Hay que determinar la cantidad de escalones que existe entre las unidades en la escalera que deseamos convertir (de metros a kilómetros, existen 3 escalones).
- Si se va de una unidad mayor a una menor se debe multiplicar por 10 la cantidad escalones hasta llegar a la unidad deseada.
- Si se va a pasar de una unidad menor a una mayor se divide por 10 la cantidad de escalones hasta llegar a la unidad deseada.
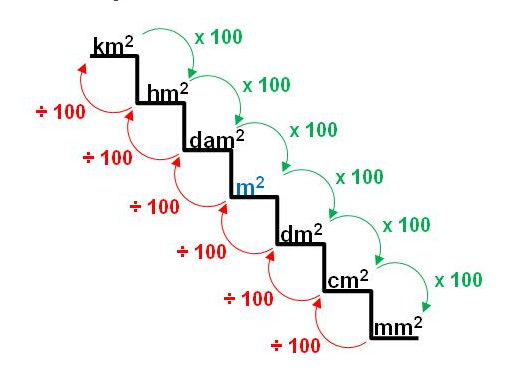
Ejemplos de las Conversiones de los Múltiplos
Si necesitáramos para de Kilómetros a metros, según la imagen de la escalera existen 3 escalones (10 x 10 x 10= 1000). Lo que significaría que se debe multiplicar la cantidad de kilómetros por 1000 y su resultado se dará en metros.
- Si vamos a viajar 3 kilómetros y necesitamos saber a cuantos metros equivalen, se realizaría la siguiente operación: 3 x 1000 = 3000 metros.
La utilización de los múltiplos es la solución matemática para evitar dar números extremadamente largos. Los cuales haría muy engorrosos los cálculos para medidas, conversiones o para dar datos exactos. Por esta razón se utiliza la potencia de 10 para brindar los datos numéricos muy largos de manera simplificada y corta. Facilitando la utilización de los datos en diversas formulas y medidas.









