Tanto en la estadística como en el campo de las probabilidades, se establece la existencia de los eventos seguros, probables o imposibles. Estos sucesos abarcar los escenarios más comunes que se puedan dar dentro de un muestreo, experimento o conjunto de datos.
Recordemos que un evento se define como los resultados que se pueden dar dentro de experimento, normalmente aleatorio. Todo esto dentro de un espacio muestral en el que se pueden presentar todos los posibles resultados, como por ejemplo al lanzar un dado.
Para lograr este tipo de resultados, es importante comprender el termino de las probabilidades. Dicho concepto fue creado en el siglo XVII por los franceses Blaise Pascal y Pierre de Fermat. Quienes la definen como el calculo que llega a medir la posibilidad de que un evento llegue a ocurrir ya sea por medio de la incertidumbre o el azar.
Se debe considerar que para lograr resultados fiables se debe definir que tipo de evento se esta considerando. Ya sea un evento aleatorio, muestral, simple, compuesto, excluyente, independiente, dependiente entre otros.
Probabilidades de los Eventos
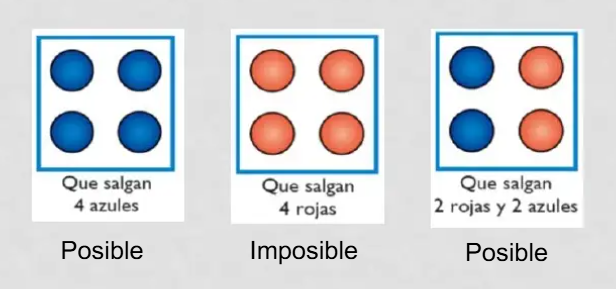
Como se indicó anteriormente las probabilidades que se pueden encontrar en los diferentes sucesos, generalmente se pueden definir como eventos seguros, probables o imposibles.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea- Evento Seguro: Se refiere a aquellos eventos en los que se da una certeza absoluta de lo que va suceder en el resultado. Por lo tanto, este resultado tendrá una probabilidad del 100%, esto significa que dentro del espacio muestral abarca todo el espacio.
- Evento Probable: También conocido como “evento posible”, se refiere a los eventos que pueden llegar a ocurrir. Sin embargo, no se posee certeza total de esto, obteniendo una probabilidad entre el 1 y el 100%. En otras palabras, en este tipo de eventos se incluyen algunos, pero no todos los resultados de la muestra.
- Evento Imposible: Son aquellos eventos en los cuales el resultado no posee ninguna posibilidad de ocurrir. Por lo tanto, su posibilidad es de un 0%.
Ejemplos de los Eventos Seguros, Probables o Imposibles
Para poder entender de una manera más clara los diversos tipos de eventos dentro de las probabilidades de los eventos.

- Evento Seguro:
- Experimento: Lanzar un dado sin trucar de 6 caras.
- Espacio de muestra (E): {1, 2, 3, 4, 5, 6}.
- Evento Segura: Lograr un resultado menor a 7. Ya que sin importar la cara del dado que caiga en el dado, su resultado siempre será menor a un 7 porque el dado solamente posee 6 caras.
- Evento Probable:
- Experimento: Lanzar un dado sin trucar de 6 caras.
- Espacio de muestra (E): {1, 2, 3, 4, 5, 6}.
- Evento Probable: Lograr un número par, Esto brinda una probabilidad de un 50% de que se logre un numero par en cada lanzamiento del dado. Tomando en consideración que los posibles resultados pares son {2, 4, 6} y poseen 3 oportunidades de 6 de salir como resultado.
- Evento Imposible:
- Experimento: Lanzar un dado sin trucar de 6 caras.
- Espacio de muestra (E): {1, 2, 3, 4, 5, 6}.
- Evento Imposible: Lograr como resultado el número 7.
Importancia de los Eventos Seguros, Probables o Imposibles
Cada uno de estos tipos de eventos poseen una importancia fundamental dependiendo de la utilidad que se les dé. A continuación, se enumeran sus principales importancias según cada uno de ellos.
- Evento seguro:
- Aplicación: Colaboran en el establecimiento del contexto según los experimentos en donde el resultado sea sin lugar a duda predecible.
- Certeza: Da la confianza de una representación del 100%, no dejando lugar para una duda en el resultado final.
- Evento Probable:
- Predicción y análisis: Ayuda a predecir futuras tendencias y permite realizar un análisis real y más exacto.
- Variabilidad: permite estudiar cada suceso dependiendo de los eventos que pueden suceder o no dependiendo de su probabilidad.
- Toma de decisiones: Permite tomar decisiones de manera informada y realista.
- Eventos Imposibles:
- Enfoque: Ayuda a determinar lo que no puede ocurrir dentro de una muestra. Por tanto, colabora en la simplificación de un problema que busca solución.
- Incertidumbre total: Representa a una ocurrencia nula en las probabilidades de una solución, dando un total del 0%.
En síntesis, la importancia de los eventos seguros, probables o imposibles, se da gracias a su utilidad para que se puedan analizar los riesgos. De esta forma se puede tomar decisiones informadas sobre predicciones en diferentes campos. Logrando de esta manera una certeza (seguro), una probabilidad o un imposible en las soluciones de la estadística, economía, finanzas o ciencias de datos.









