Los números poseen una gran variedad de representaciones como lo son los números reales, complejos, racionales, irracionales, enteros y naturales. Su interacción se vuelve tangible al realizar diversas operaciones con números en sus diferentes representaciones.
Esto indica que, aunque parezca que cada representación es muy diferente a otra como en los números positivos, negativos, raíces, potencias, decimales, fracciones entre otras. Y con la utilización de paréntesis, operaciones básicas, exponentes o interrogantes. Se pueden utilizar dentro de la misma operación matemática.
Para encontrar la solución de la operación en este tipo de circunstancias, es importante seguir las reglas y el orden de solución de cada una de las operaciones. Dicho orden se realiza por una jerarquía que se conoce abreviadamente como PEMDAS o PAPOMUDAS.
Conocer y respetar el orden de la resolución de operaciones es igual de vital que el conocer cada uno de las diferentes representaciones de los números. De igual manera es importante conocer el comportamiento de los símbolos en cada número y si reacción ante una operación básica.
Orden de las operaciones PEMDAS / PAPOMUDAS
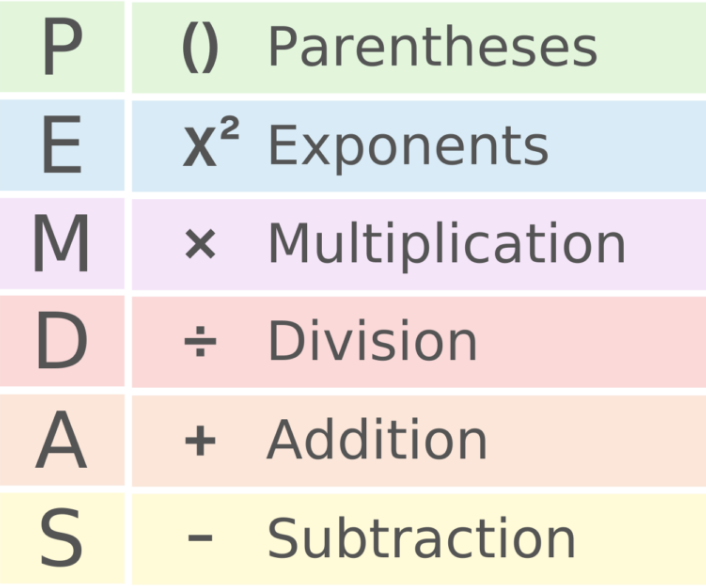
A la hora de iniciar el desarrollo de las operaciones con números en sus diferentes representaciones, se debe tener claro la jerarquía de la resolución. Dicho orden se ha establecido para que de manera organizada se vaya logrando una solución adecuada de una operación matemática.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea- PEMDAS:
- P: Paréntesis.
- E: Exponente y raíces.
- M: Multiplicaciones.
- D: División.
- A: Adición o suma.
- S: Sustracción o resta.
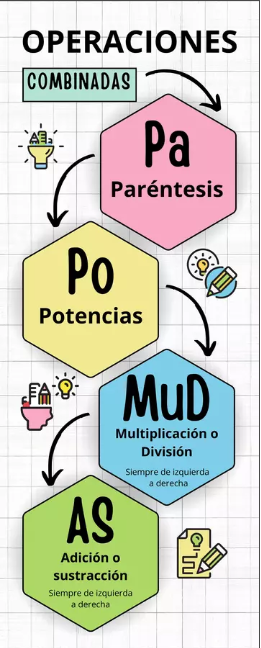
- PAPOMUDAS:
- PA: Paréntesis.
- PO: Potencias.
- MU: Multiplicación.
- D: División.
- A: Adición o suma.
- S: Sustracción o resta.
En el caso de los paréntesis se inicia su resolución por el que este más adentro y de ahí avanza hacia afuera. Existen tres tipos de paréntesis los cuales son:
- Redondos ().
- Cuadrados [].
- Corcheas {}.
Los Signos en Operaciones con Números en sus Diferentes Representaciones
De la misma manera que sucede en la jerarquía de las operaciones en cada número se debe tener presente si este es positivo o negativo. Esto ya que la interacción de los signos con las operaciones básicas puede afectar directamente el signo que llevara el número en el resultado.

- Suma y Resta: Cuando se habla de la adición y sustracción de los signos, se debe tener en cuenta que si ambos signos son iguales se conserva el signo. Pero si los signos son distintos, se conserva el signo del número mayor.
- Mismo Signo: En caso de signos negativos (-5) + (-3) = -8. En caso de la suma 7+5= 12.
- Signos Diferentes: En este caso se resta el valor menor al mayor y se conserva el signo del mayor. Ejemplos 7 + (-5) = 2, si el mayor es positivo y -10 + 3 = -7 en caso de se el mayor un número negativo.
- Multiplicación y División: En estas dos operaciones si los signos son iguales el resultado será positivo, mientras que si son diferentes el resultado será negativo. Esta regla se aplica de igual manera en la división.
- Mismo Signo: El resultado es positivo, ambos signos son iguales. Ejemplo: 5 x 4 = 20, en caso de números positivos y en el caso de números negativos (-3) x (-6) = 18.
- Signos Diferentes: En este caso el resultado será negativo. Ejemplo: -3 x 6 = -18 // 5 x (-4) = -20.
- Regla de signos:
- (+) x (+) = (+).
- (+) x (-) = (-).
- (-) x (-) = (-).
- (-) x (+) = (-).
Reglas y Procedimientos de las Operaciones con Números en sus Diferentes Representaciones
Como se ha indicado anteriormente lo primero que se debe respetar duranta las operaciones con números en sus diferentes representaciones es el orden PEMDAS. Sin embargo, también debemos estar consientes de cuales son las representaciones de los números con las que vamos a trabajar.
De esta manera se podrán realizar las conversiones, despejes o simplificaciones necesarias para que sea más sencillo realizar las operaciones durante su desarrollo. También es importante conocer en cual representación nos están solicitando la respuesta o solución.
Por ejemplo, se puede pasar los números de fracciones a decimales o números enteros, de igual forma se pueden despejar las raíces o las potencias. De esta manera se trabajaría en la misma línea tipo de números y facilitar su uso en las operaciones.
Ejemplos de Operaciones con Números en sus Diferentes Representaciones
- 7- 4 x 2 + 9 =
7 -8 + 9 = 8.
- 55 -6 x (3 +1) -5² =
55 -6 x 4 -5² =
55 -24 – 25 = 6.
- 3 x 24/6 – (√4 + 2,5²) =
3 x 4 – (√4 + 2,5²) =
12 – (2 + 6,25) = 3,75.
Las Operaciones con Números en sus Diferentes Representaciones son importantes ya que establecen las reglas y el orden para su correcta resolución. De esta manera se puede resolver problemas complejos, fomentando la habilidad del calculo de manera precisa al igual que el razonamiento lógico.









