Otro ejemplo de las medidas de posición es el de la media aritmética, la cual se obtiene de la suma de todos los valores que conformen una base de datos. Para después dividir el resultado por la cantidad en total de esos valores. A este tipo de medida también se le conoce como “promedio” o simplemente como “media”.

La media aritmética puede ser muy utilizado en campos como la estadística, la matemática, economía, historia, antropología y en casi todos los campos académicos existentes. Su actuar se encuentra muy influida por valores atípicos (los valores mayores o menores que la mayoría de los demás), por esta razón no es considerada como una estadística robusta.

La mediana por otra parte si es considerada como una estadística robusta, lo que explicaría que, en la distribución de la renta, la mediana puede dar una descripción más exacta que la que puede brindar la media aritmética.

Fórmula de Cálculo de la Media

Para lograr el correcto calculo de un promedio es necesario seguir los siguientes pasos:

• Se debe tomar todos los valores que conformen el conjunto de datos y sumarlos.
• Es importantes que se conozca con exactitud la cantidad de valores que se encuentran en total dentro del conjunto de datos.
• Al obtener el resultado de la suma se debe dividir por la cantidad de valores que conformen el conjunto.
• Al resultado de la división se le conocerá como media aritmética.

Para entender de una mejor manera la aplicación de la operación y su formula se puede dar el siguiente ejemplo: Si se debe conocer el promedio de los números 2,3,3,5, 7 y 10.

• Sumar los valores: 2+3+3+5+7+10= 30.
• Cantidad de valores: 6 valores en total.
• División: 30 / 6= 5.
• La media aritmética corresponde a 5.

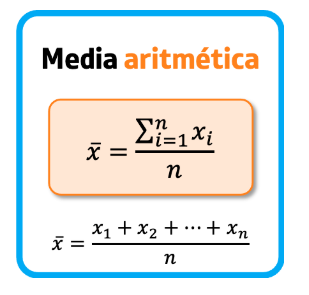
Matemáticamente la formula utilizada para obtener la media se puede visualizar de la siguiente manera:

X = Σxi / N

X= Media aritmética.

Σxi= Es la suma de los valores.

/= Signo de división.

N= Cantidad total de valores.

Diferencia entre la Media Aritmética y la Mediana

Ambas pertenecen en conjunto con la Moda a las medidas de posición, pero sin embargo poseen varios contrastes entre una y otra. La mediana es aquel valor central existente en un conjunto de datos que se ordenan de menor a mayor.

Por otra parte, la media aritmética es el promedio existente en la suma de los valores y la división entre la cantidad de dichos valores. La principal diferencia que radica entre ambos es que mientras la media es afectada por aquellos valores atípicos. Mientras que la mediana es más robusta y puede representar de una mejor manera el centro de los datos que no se distribuyen uniformemente (sesgados).

Propiedades de la Media Aritmética Claves

• Punto de equilibrio: La media representa al punto en que se equilibran la distribución de los datos del conjunto.
• Suma de desviaciones: Dicha suma con respecto a la media, siempre tendrá como resultado “cero”. En otras palabras, la suma que se da de las diferencias entre cada dato y la media siempre será cero.
• Valores atípicos: La media es sumamente sensible a aquellos valores considerados como atípicos o extremos dentro del conjunto de datos. Si se llega a dar un valor muy alto o muy bajo podría distorsionar el resultado del promedio.
• Desviaciones cuadradas mínima: Al sumar la diferencia y elevarlas al cuadrado de cada valor con respecto a la media, esta es la mínima posible en comparación con cualquier otro punto.
• Unicidad: Se puede considerar a la media aritmética como el valor único de cualquier conjunto de datos.
• Suma y resta de constantes: Al sumar o restar un valor que sea constante en todos los datos de un conjunto, la media se sumara o restara de igual manera a la misma constante.
• Multiplicar o dividir constantes: Si los valores son multiplicados o divididos por una constante distinta a “cero”, el resultado de la media será el mismo de multiplicar o dividir la media por esa misma constante.
• Posición intermedia: Se puede decir que la media siempre se ubicara entre el valor más grande y el más pequeño dentro del conjunto de datos.
• La media se ve influenciada directamente por cada uno de los valores del conjunto de datos.

Utilidad de la Media Aritmética

Es acertado indicar que la media aritmética se puede utilizar con gran frecuencia e importancia en el campo del marketing, finanzas, educación, economía, ciencias sociales, entre muchas otras. Su utilizar se puede traducir de la siguiente manera:

• Caracterizar y resumir los datos: Se brinda un valor representativo, el cual puede resumir la tendencia central de la base de datos. Resumiendo, de esta manera la información compleja.
• Evaluación y Análisis: Permite evaluar y analizar los datos de una manera que facilite la toma de decisiones ya que se basara en la evidencia.
• Toma de Decisiones: Permite entender el comportamiento general de todo el conjunto de datos, por tanto, brinda información crucial para realizar una toma de decisiones informada dependiendo del contexto de los datos.
• Punto de Referencia: Puede actuar como un punto de referencia al evaluar y comparar los distintos datos que se presentan dentro del conjunto.

Se esta manera la media aritmética que puede llegar a convertir en una herramienta esencial dentro del campo de la estadística descriptiva. Esto permite una discusión y análisis más profundos sobre la distribución de los datos y las capacidades analítica y critica. De esta manera se permite interpretar de una mejor manera la información que se brinda.