Las relaciones numéricas de fracciones se refieren a las conexiones y comparaciones entre diferentes fracciones. Estas relaciones se pueden expresar de varias maneras, como mediante equivalencias, comparaciones de tamaños, operaciones aritméticas y representaciones en diversas formas.

La interpretación de las fracciones como relación parte-todo se produce cuando un todo (continuo o discreto) se divide en partes iguales. La fracción (propia) indica la relación existente entre el todo, que recibe el nombre de unidad y el número de partes que se consideran de dicha unida.

La importancia de las relaciones numéricas de fracciones

Las relaciones numéricas de fracciones son fundamentales en matemáticas porque permiten comprender y trabajar con cantidades que no son enteras. Las relaciones numéricas de fracciones son esenciales para una amplia gama de aplicaciones prácticas y teóricas y su comprensión es crucial para el desarrollo de habilidades matemáticas avanzadas y la resolución efectiva de problemas en la vida diaria.

• Comprensión de las proporciones y razones:
  • Las fracciones son esenciales para entender las proporciones y las razones, lo que es crucial en muchas áreas, como la cocina, la química y la economía.
• Resolución de problemas:
  • Las fracciones permiten resolver problemas que involucran partes de un todo. Esto es útil en situaciones como dividir una pizza entre varias personas o calcular descuentos y porcentajes en compras.
• Matemáticas avanzadas:
  • El dominio de las fracciones es un paso fundamental para avanzar en matemáticas más complejas, como álgebra, cálculo y estadística. Las fracciones ayudan a entender conceptos como la pendiente de una línea y la integración de funciones.
• Conversión entre unidades:
  • Las fracciones facilitan la conversión entre diferentes unidades de medida. Por ejemplo, convertir pulgadas a centímetros o millas a kilómetros a menudo implica trabajar con fracciones.
• Interpretación de datos:
  • En ciencias y estadísticas, los datos a menudo se presentan como fracciones o porcentajes. Entender las relaciones numéricas de fracciones ayuda a interpretar estos datos de manera precisa.
• Equidad y reparto justo:
  • Las fracciones son útiles para garantizar una distribución equitativa de recursos. Por ejemplo, dividir herencias, repartir ganancias o asignar tiempos equitativos en turnos de trabajo a menudo involucra el uso de fracciones.
• Comprensión del valor relativo:
  • Las fracciones permiten comparar cantidades y entender el valor relativo de diferentes números. Por ejemplo, saber que 3/4 es mayor que 2/3, o que 1/2 es igual a 2/4, ayuda a tomar decisiones informadas en contextos cotidianos.

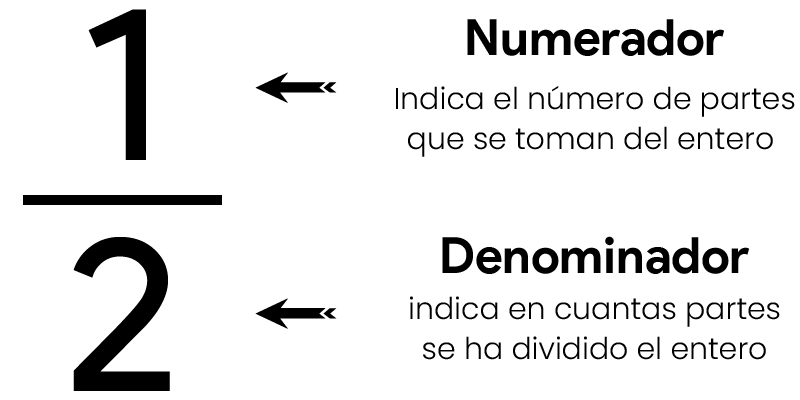
¿Qué es el numerador y denominador en las fracciones?

En una fracción, el numerador es el número en la parte superior que indica cuántas partes del todo se están considerando, mientras que el denominador es el número en la parte inferior, que muestra en cuántas partes iguales se ha dividido el todo.

• Numerador:
  • Es el número que se encuentra en la parte superior de la fracción. Representa cuántas partes del todo estamos considerando. Por ejemplo, en la fracción 3/4 el numerador es 3, lo que indica que tenemos 3 partes de un total.
• Denominador:
  • Es el número que se encuentra en la parte inferior de la fracción. Indica en cuántas partes iguales se ha dividido el todo. En la fracción 3/4 el denominador es 4, lo que significa que el todo se ha dividido en 4 partes iguales.
• La fracción completa 3/4 se interpreta como (tres cuartos), lo que significa que estamos considerando tres partes de un total dividido en cuatro partes iguales.

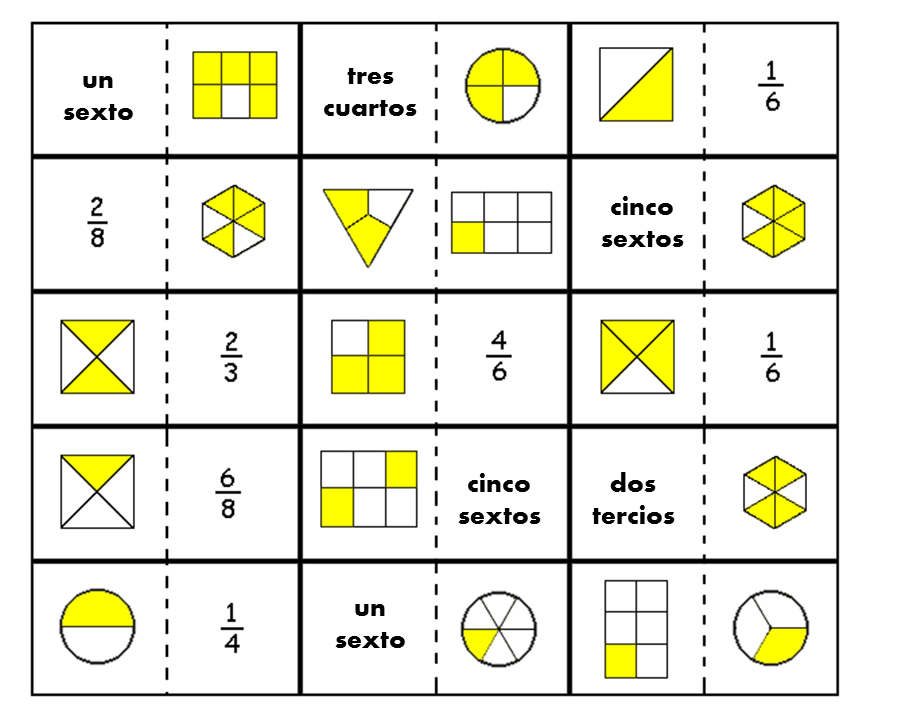
¿Cuál serían las relaciones numéricas de fracciones?

Las relaciones numéricas de fracciones se refieren a las conexiones y comparaciones entre diferentes fracciones. Estas relaciones se pueden expresar de varias maneras, como mediante equivalencias, comparaciones de tamaños, operaciones aritméticas y representaciones en diversas formas.

• Equivalencia de Fracciones:
  • Dos fracciones son equivalentes si representan la misma cantidad.
    • Por ejemplo 1/2 y 2/4
    • Si tomamos la primera facción y la dividimos 1÷2 = 0,5 al igual que si tomamos 2÷4= 0,5 en ambos casos es el mismo resultado. Se multiplica en cruz para saber son equivalentes 1×4= 4 2×2=4 la fracción sería 4/4 se lee (cuatro cuartos)
• Comparación de Fracciones:
  • Las fracciones pueden compararse para determinar cuál es mayor, menor o si son iguales.
  • Usando estos signos (> < o =)
• Operaciones Aritméticas con Fracciones:
  • Suma: Para sumar fracciones, es necesario encontrar un denominador común.
    • Ejemplo: 1/3 + 1/4 primero mutiplicamos 3×4 = 12 para sacar un denominar y luego multiplicamos 1×4 = 4 1×3= 3 estos resultados los sumanos 4+3 = 7 la fracción quedaría asi 7/12 se lee (siete doceavos)
  • Resta:
    • Ejemplo de Resta de Fracciones, restemos 3/4 y 1/4 verifica los denominadores y son iguales (ambos son 4) se dejan así. Restamos los numeradores 3-1= 2 la fracción sería 2/4 se lee (dos cuartos)
    • La fracción 2/4 se puede simplificar dividiendo el numerador y el denominador por su máximo común divisor (2): 2÷1= 1 y 4÷2 =2 entonces 1/2 se lee (un medio)
  • Multiplicación:
    • Se multiplican los numeradores entre sí y los denominadores entre sí. Ejemplo: las fracciones 2/3 y 3/4 la primera es 2×3= 6 y 3×4= 12 la fracción quedaría así 6/12 se lee (seis doceavos).
  • División:
    • Se multiplica la primera fracción por el recíproco de la segunda. Ejemplo: 2/3 y 3/4 2×4=8 3×3=9 en la primera quedaria 8/9 se lee (ocho novenos)

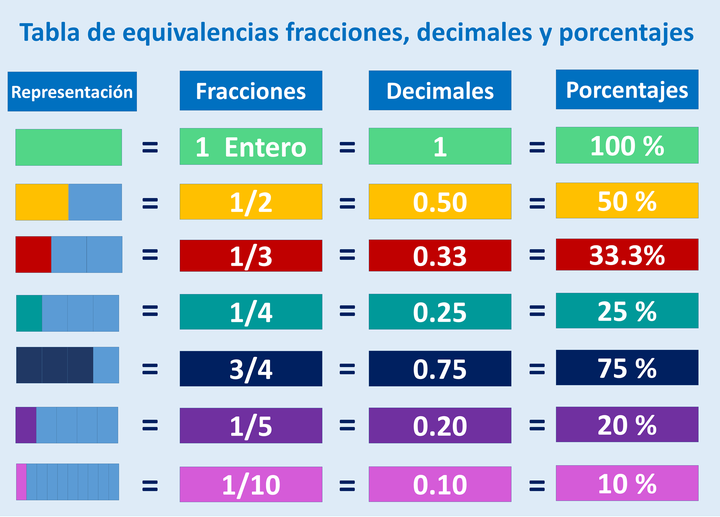
¿Qué es la relaciones numéricas de fraciones en porcentajes?

Recuerde que un porcentaje es realmente solo una forma especial de expresar una fracción como un número de 100. Para convertir una fracción en un porcentaje, primero divida el numerador entre el denominador y luego multiplique el decimal por 100. La fracción 4/8 puede ser convertida a un decimal al dividir 4 entre 8. Puede ser convertida en un porcentaje al multiplicar el decimal por 100.

• Ejemplos 1:
  • Tomamos la fracción 4/8 y la dividimos entre 4÷8 = 0.5 el resultado de esta división la multiplicamos
    • → 0.5×100 = 50%
• Ejemplo 2:
  • Tomamos la fracción 2/5 y la dividimos entre 2÷5 = 0.4 el resultado de esta división la multiplicamos
    • ​→ 0.4×100 = 40%
• Ejemplo 3:
  • Tomamos la fracción 3/4 y la dividimos entre 3÷4 = 0.75 el resultado de esta divición la multiplicamos
    • → 0.75×100 = 75%
• Ejemplo 4:
  • Tomamos la fracción 7/10 y la dividimos entre 7÷10 = 0.7 el resultado de esta divición la multiplicamos
    • → 0.7×100 = 70%

Dominando las operaciones matemáticas

Dominar las operaciones matemáticas con fracciones es esencial para el desarrollo de habilidades avanzadas en matemáticas y otras disciplinas relacionadas. Las fracciones representan partes de un todo y son fundamentales para comprender conceptos más complejos de las matemáticas, al aprender a sumar, restar, multiplicar y dividir fracciones no solo mejora la capacidad de resolver problemas matemáticos, sino que también facilita el entendimiento de situaciones cotidianas donde se manejan porciones y proporciones.

Recuerden que las fracciones son una herramienta poderosa en matemáticas. Ya sea que estén cocinando, midiendo algo, o resolviendo problemas más complejos, comprender las relaciones numéricas de las fracciones les dará una ventaja para soluccionar cualquier operación matemática y siempre debemos disfrutar el proceso de aprendizaje que llevará a lograr nuestras metas.