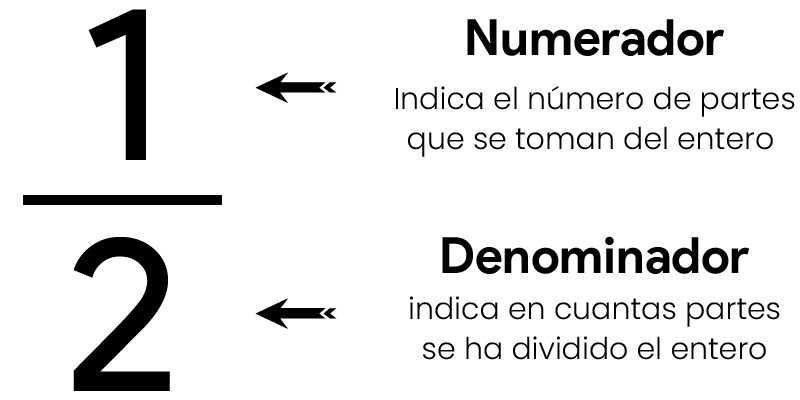
Las fracciones heterogéneas o fracciones no equivalentes, son aquellas que tienen diferentes denominadores. Esto significa que el numerador puede ser igual, la fracción no representa la misma cantidad que otra fracción con un denominador diferente. Para comparar o sumar, restar estas llamativa fracción, es necesario encontrar un denominador común.

Características de las fracciones heterogéneas

Las fracciones heterogéneas tienen denominadores diferentes, lo que impide operarlas directamente. Para sumarlas o restarlas, es necesario encontrar un denominador común y convertirlas en fracción equivalente.

Las heterogéneas tienen varias características distintivas:

• Diferentes denominadores:
  • La característica principal es que las fracciones tienen denominadores diferentes. Esto significa que las partes en las que se divide la unidad no son del mismo tamaño.
• No se pueden operar directamente:
  • Los denominadores son diferentes. No se puede sumar, restar o comparar directamente. Es necesario convertirlas en fracciones homogéneas (con el mismo denominador) para realizar estas operaciones.
• Necesitan un denominador común:
  • Para operar con fracciones heterogéneas, es necesario encontrar un denominador común. El denominador común suele ser el mínimo común múltiplo (MCM) de los denominadores originales.
• Proceso de conversión:
  • Para convertir fracciones heterogéneas enhomogéneas, se multiplica el numerador y el denominador de cada fracción y el número necesario para obtener el denominador común.
• Comparación más complicada:
  • Relacionar las fracciones heterogéneas a una comparación con las homogéneas, es necesario llevarlas a un denominador común y comparar los numeradores.
• Aplicación en problemas complejos:
  • En muchos problemas matemáticos, que involucran suma, resta o comparación, se requiere convertir fracciones heterogéneas a homogéneas para simplificar los cálculos.

¿Cuáles son las fracciones heterogéneas?

Las fracción heterogénea son aquellas que tienen diferentes denominadores. Para realizar operaciones con ellas, sumar, restar o comparar, es necesario encontrar un denominador común. En el caso de la multiplicación y la división, no es necesario encontrar un denominador común, en estas operaciones se pueden realizar directamente sobre las fracciones originales.

• Ejemplo 1:
  • Suma.
    • Analicemos | ⅔ y ¾
  • Encuentra un denominador común: El mínimo común múltiplo (MCM) de 3 y 4 es 12.
    • ⅔ mutiplicamos 2×4= 8 3×4= 12 la fracción es 8/12 despúes ¾ 3×3= 9 4×3= 12 la fracción es 9/12
  • Suma las fracciones:
    • Sumamos los numeradores 8+9=17 y el denominador queda igual 12
      • Resultado final es 17/12
• Ejemplo 2:
  • Resta.
    • Analicemos | 7/8 y 2/5
  • Encuentra un denominador común: El MCM de 8 y 5 es 40.
    • Convierte las fracciones:
      • 7/8 mutiplicamos 7×5 = 35 y 8×5= 40 la fracción es 35/40 y 2/5 2×8=16 5×8= 40 la fracción es 16/40
  • Resta las fracciones:
    • Restamos 35-16 = 19 y el denominador queda igual
      • Resultado final es 19/40
• Ejemplo 3:
  • Comparación de fracciones heterogéneas
    • Compararemos para saber cual es mayor | 5/6 y 3/7
      • Encuentra un denominador común: El MCM de 6 y 7 es 42.
    • 5/6 multiplicamos 5×7=35 y 6×7=42 la fracción es 35/42 y 3/7 3×6= 18 y 7×6=42 l fracción es 18/42
      • Resultado 5/6 es mayor que 3/7 representado 35/42 > 18/42
• Ejemplo 4:
  • Multiplicación.
    • Multipliquemos 4/9 y 3/7
      • Multiplica numeradores y denominadores 4×3=12 y 9×7= 63 la fracción es 12/63
    • Simplifica la fracción
      • dividimos numerador 12÷3= 4 y denominador 63÷3=21 la fracción simplificada 4/21.
• Ejemplo 5:
  • División.
    • Dividamos 5/8 entre 2/3
    • Multiplica 5×3=15 y 8×2= 16 la fraccíon es 15/16
      • Dividimos 5÷3= 5 y 8÷2= 4 la fracción es 5/4

No subestimemos las fracciones en la educación matemática

Las fracciones heterogéneas son un importante concepto en el aprendizaje de las matemáticas. Son fracciones que tienen diferentes denominadores, lo que les permite representar partes de un todo que no se dividen en la misma cantidad. A través de su estudio y comprensión, los estudiantes pueden desarrollar habilidades para comparar, ordenar y operar con estas fracciones, lo que les dará una base sólida para el aprendizaje de conceptos más avanzados en álgebra y cálculo. Las fracciones tienen aplicaciones prácticas en la vida cotidiana, para realizar mediciones o repartir cantidades entre varias personas.

Trabajar con fracciones heterogéneas es un paso crucial en el dominio de las matemáticas. Al encontrar un denominador común, transformamos fracciones complejas en expresiones manejables y resolvemos problemas que parecerían intrincados. Esta habilidad no solo es fundamental en el ámbito académico, nos ayudarán con prácticas en la vida diaria, desde dividir cantidades hasta comparar proporciones.