En la matemática la división es una operación parcialmente definida en el conjunto de los números enteros y su signo es (÷). En cambio, en el caso de los números racionales, reales y complejos es siempre posible efectuar la división. Exigiendo que el divisor sea distinto de cero, sea cual fuera la naturaleza de los números por dividir.
La importancia de la División en matemáticas
La división es una de las operaciones fundamentales en matemáticas y desempeña un papel crucial en diversas áreas del conocimiento. Es una herramienta que permite descomponer números y entender cómo se relacionan entre sí, proporcionando el camino hacia otros conceptos matemáticos como fracciones, porcentajes y proporciones.
A través de la división es posible repartir recursos de manera equitativa, calcular tasas, así como resolver ecuaciones y simplificar expresiones algebraicas. En la educación básica, la comprensión de la división ayuda a desarrollar habilidades de resolución de problemas y a consolidar la base para el aprendizaje de matemáticas avanzadas.
Partes de la división
En matemáticas, la división es una operación que consiste en dividir un número por otro para obtener un resultado. Esta operación se compone de cuatro partes fundamentales, las mismas son de gran importancia para entender y realizar la operación de división en matemáticas.
Las cuatro partes principales en una división:
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea- Dividendo:
- Es el número que se va a dividir.
- Divisor:
- Es el número por el cual se va a dividir el dividendo.
- Cociente:
- Es el resultado de la división.
- Residuo (o Resto):
- Es lo que queda después de dividir el dividendo por el divisor.
Introducción de la División
La forma más sencilla de ver la división es en términos de «cociente y partición»: desde el punto de vista del cociente, 20 / 5 significa el número de 5s que hay que sumar para obtener 20. Desde el punto de vista de la partición, 20 / 5 significa el tamaño de cada una de las 5 partes en que se divide un conjunto de tamaño 20.
Por ejemplo, 20 manzanas se dividen en cinco grupos de cuatro manzanas, lo que significa que veinte dividido por cinco es igual a cuatro. Esto se denota como 20 / 5 = 4. Lo que se divide se llama el dividendo, que se divide por el divisor y el resultado se llama el cociente. 20 es el dividendo, 5 es el divisor y 4 es el cociente.
¿Cuál es la División de números enteros?
La división de números enteros es una operación matemática básica donde se divide un número entero por otro para obtener un cociente y en algunos casos, un residuo. (Cociente) el resultado principal de la división. (Residuo) lo que queda si el divisor no divide completamente al dividendo.
Aquí hay algunos puntos clave sobre la división de números enteros:
- División exacta: Si el dividendo es un múltiplo exacto del divisor, no hay residuo.
- División con residuo: Si el dividendo no es un múltiplo exacto, el residuo será la parte que sobra después de la división.
- División exacta:
- 10 ÷ 2 = 5. No hay residuo porque 10 es divisible por 2.
- División con residuo:
- 10 ÷ 3 = 3 con residuo 1. El cociente es 3 porque 3 x 3 es 9, pero 10 – 9 es 1, que es el residuo.
- Relación entre cociente y residuo: La relación se puede expresar con la fórmula 𝑎 = (𝑏×𝑞) + 𝑟 Donde:
- a es el dividendo
- b es el divisor
- q es el cociente
- r es el residuo
¿Cuál es la División de números racionales?
La división de números racionales es el proceso de dividir una fracción por otra. Se logra al multiplicar la primera fracción por el inverso de la segunda. El inverso de una fracción se obtiene intercambiando su numerador y denominador.
Aquí tienes cuatro ejemplos de números racionales:
- Ejemplo 1:
- Si tienes 3/4 de un pastel y necesitas dividirlo entre 2/3 de otra porción, el resultado es cuánto pastel tiene cada persona después de dividir entre esa porción. Para dividir, tomas el inverso de 2/3 (que es 3/2) y lo usas para multiplicar el 3/4. El resultado es 9/8 de un pastel.
- Ejemplo 2:
- Si tienes 5/7 de un galón de pintura y quieres dividirlo entre 1/3 de otro galón, para saber cuántas veces cabe la segunda porción en la primera, necesitas tomar el inverso de 1/3 (que es 3). Luego, multiplica el 5/7 por ese inverso. El resultado es 15/7, o 2 y 1/7 galones.
- Ejemplo 3:
- Si tienes 7/9 de una receta y quieres dividirlo entre 3/4 de otra receta para saber cuántas veces cabe la segunda receta en la primera, necesitas invertir 3/4 (que es 4/3) y multiplicar por 7/9. El resultado es 28/27, que es un poco más que 1 receta.
- Ejemplo 4:
- Si tienes 2/5 de un tanque de gasolina y necesitas dividirlo entre 4/7 de otro tanque, para saber cuánto obtendrás, inviertes 4/7 (que es 7/4) y multiplicas por 2/5. El resultado es 14/20, que simplificado es 7/10 del tanque.
¿Cuál es la División de números enteros?
La división de números enteros es el proceso de encontrar cuántas veces un número (el divisor) cabe en otro número (el dividendo). En términos simples, es responder la pregunta: ¿Cuántas veces cabe un número en otro?
- Ejemplo 1:
- Dividendo: 12
- Divisor: 4
- Resultado: 3
- Residuo: 0
- Explicación: Al dividir 12 entre 4, el resultado es 3, porque 4 cabe exactamente tres veces en 12.
- Ejemplo 2:
- Dividendo: 15
- Divisor: 2
- Resultado: 7
- Residuo: 1
- Explicación: Si divides 15 entre 2, el resultado es 7 porque 2 cabe siete veces en 15. El residuo es 1, porque 15 – (2 x 7) = 1.
- Ejemplo 3:
- Dividendo: 20
- Divisor: 6
- Resultado: 3
- Residuo: 2
- Explicación: Al dividir 20 entre 6, el resultado es 3, porque 6 cabe tres veces en 20. El residuo es 2, porque 20 – (6 x 3) = 2.
- Ejemplo 4:
- Dividendo: 100
- Divisor: 10
- Resultado: 10
- Residuo: 0
- Explicación: Dividiendo 100 por 10, el resultado es 10, porque 10 cabe diez veces en 100. No hay residuo.
Resultado de dividir entre cero
La división por cero es una “indefinición” porque no tiene sentido en matemáticas. Cuando dividimos un número, queremos saber cuántas veces un divisor cabe en un dividendo. Pero con cero, no hay una respuesta clara porque cualquier número multiplicado por cero da cero. Este hecho crea problemas cuando tratamos de dividir un número por cero.
Otra forma de verlo es que la división es el proceso inverso de la multiplicación. Para cualquier número diferente de cero, existe un inverso multiplicativo. Pero el cero no tiene inverso multiplicativo, lo que significa que no hay ningún número que, al multiplicarse por cero, nos dé algo distinto de cero.
El papel crucial de la multiplicación
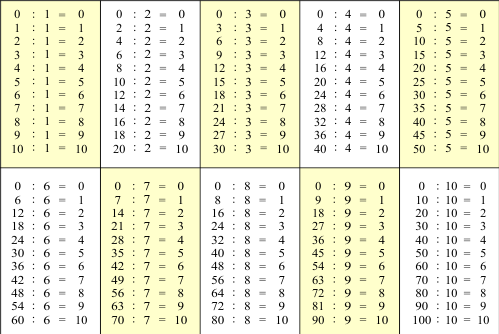
Para dividir, necesitas tener un buen conocimiento de la multiplicación. Esto se debe a que la división es el proceso inverso a la multiplicación. Al conocer las tablas de multiplicar, puedes entender mejor cómo encontrar cuántas veces un número cabe en otro.
Supongamos que tienes 20 y quieres dividirlo por 4. Si sabes que 4 por 5 es 20, entonces puedes inferir que 20 dividido por 4 es 5. Esta comprensión proviene del conocimiento de las tablas de multiplicar.
La división es mucho más que una simple operación aritmética; es una herramienta que nos ayuda a comprender y abordar el mundo de manera más eficaz. Practicar y entender la división nos prepara para desafíos más grandes y nos da las bases para explorar conceptos matemáticos avanzados









