Después de las ecuaciones lineales, dentro de la matemática se encuentran las ecuaciones de segundo grado. Las cuales también son conocidas como las ecuaciones cuadráticas, se componen de polinomio en donde la incógnita o variable, posee un exponente de dos (máximo).
De una manera general las ecuaciones cuadráticas se pueden expresar de manera general de la siguiente manera: ax² + bx + c = 0. En este caso la “a” no puede ser “0” (cero), su solución se logra por medio de la factorización o de la formula cuadrática general.
Las ecuaciones de segundo grado pueden presentar una o dos soluciones reales, incluso puede no tener ninguna. Las soluciones dependen del valor que posee el discriminante, el cual corresponde a la parte dentro de la raíz cuadrada en la formula de la ecuación.

Componentes de la Ecuación Cuadrática
Según la forma de las ecuaciones de segundo grado se puede indicar cada uno de sus componentes de la siguiente manera: ax² + bx + c = 0.
- a: Corresponde al coeficiente del término cuadrático (x²).
- b: Se refiere al coeficiente del término lineal (x).
- c: Este corresponde al termino constante o independiente.
- x: Se identifica con la variable o incógnita.
- Importante Condición: El valor de a nunca debe ser cero (a≠0).
Historia de las Ecuaciones de Segundo Grado
Las ecuaciones de segundo grado tienen sus raíces desde hace muchos años, ya que desde la antigua Babilonia se tenían algoritmos capaces de resolverla. El matemático Diofanto de Alejandría desde Grecia aporto una manera de solucionarla, pero solamente brindaba una solución a la ecuación.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en líneaPero fue hasta que Al-Juarisimi, durante el siglo IX, pudo aportar de manera completa el desarrollo para la solución de las ecuaciones cuadráticas. Más tarde Évariste Galois contribuye con la solución de las ecuaciones con polinomios.
Una de las dificultades que la resolución de estas ecuaciones se dio al evaluar x² -2 =0, durante la época de los estudiantes de Pitágoras. Ya que al calcular la longitud de la diagonal en un cuadrado de lado 1 y al no poder expresar la raíz cuadrada de 2 como la razón de 2 números enteros.
Durante el Renacimiento al intentar resolver x² +1 = 0, se necesitaba encontrar un numero real cuyo cuadrado sea -1. Fue gracias a la creación de los números imaginarios y la invención de la unidad “i” que define la igualdad i²= -1.
Naturaleza de las Raíces del Discriminante
Cuando nos referimos a un discriminante, nos referimos a Δ= b² -4ac, que sirve para poder analizar los tipos de naturalezas de las raíces, ya sean complejas o reales.
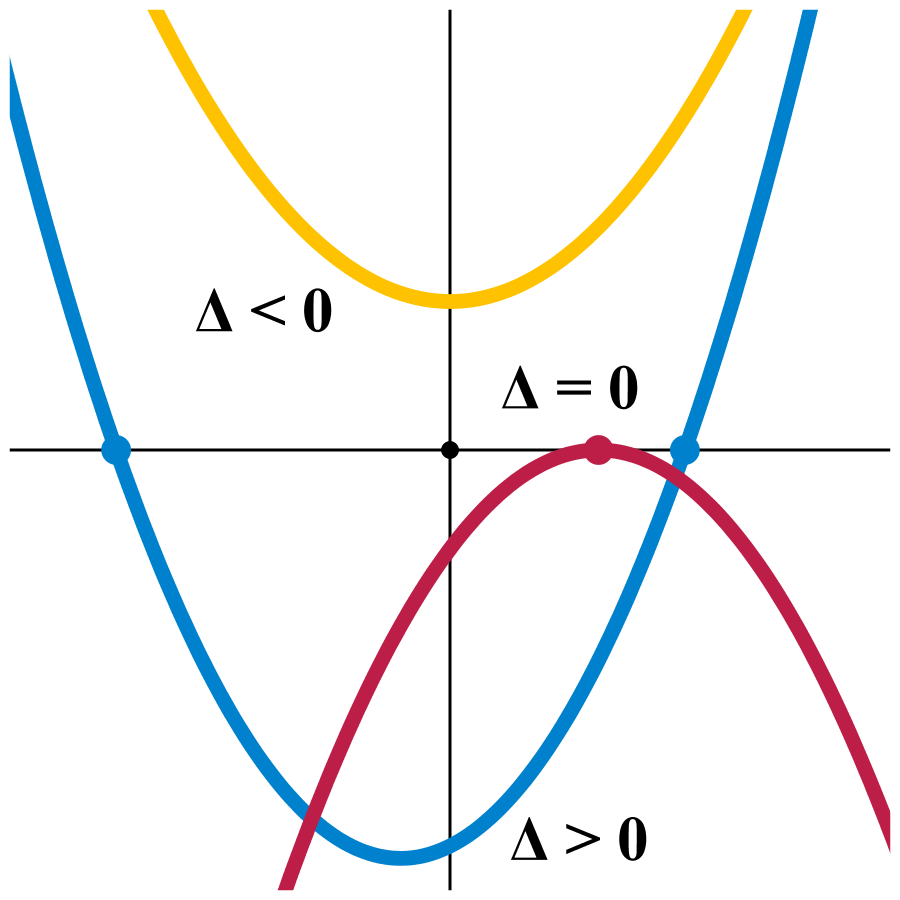
- Δ>0 : Establece dos raíces reales distintas, esto quiere decir que la parábola corta el eje en dos puntos distintos. En otras palabras, posee dos soluciones reales distintos.
- Δ<0 : Indica dos raíces complejas conjuntas, en este caso la parábola no corta el eje. No posee soluciones reales, pero si complejas.
- Δ=0 : Posee una raíz real, pero con multiplicidad de dos o doble, en este caso la parábola solamente toca un punto en el eje. Solamente posee una única solución o dos si son iguales.
Tipos de Ecuaciones Cuadráticas
- Ecuaciones Completas: Son aquellas en las que a, b y c son diferentes a 0 (cero).
- Ecuaciones Incompletas: Se dan cuando b=0 (ecuación bi-cuadrática) o si c=0 (ecuación de binomio).
Resolución de Ecuaciones de Segundo Grado
- Completar el Cuadrado: Se usa con la identidad algebraica de x²+ 2hx + h² = (x+h) ². Representa al algoritmo definido que es usado por lo general para resolver cualquier ecuación de segundo grado. Esto siempre y cuando se parta de la forma estándar ax² + bx + c = 0.
- Cada lado se debe dividir por a (coeficiente del término elevado al cuadrado).
- Se debe restar el termino constante c/a en ambos lados.
- Añadir el coeficiente de x a ambos lados del cuadrado de la mitad de b/a. Completando el cuadrado y formando un “cuadrado perfeto”.
- Simplificar el lado derecho, escribiendo el lado izquierdo como un cuadrado.
- Para igualar la raíz cuadrado izquierdo con raíces cuadradas (negativa y positiva) del lado se debe producir dos ecuaciones lineales.
- Resolver las ecuaciones lineales.
- Ejemplo: 2x² +4x -4 = 0

x2+2x−2=0

x2+2x=2

x2+2x+1=2+1

(x+1)2=3

x+1=±3

x=−1±3

Nota: el signo de ± significa que el termino puede ser positivo o negativo. Ahora que para encontrar el corte en la parábola se utiliza la siguiente formula para el eje x: f(x)=0; ax² +bx + c = 0.
Factorización
Implica que se tiene que reescribir las ecuaciones de segundo grado, como el producto de dos factores lineales.
- Buscar como expresar ax² + bx + c, como (px + q)(rx+s).
- Usando la propiedad del producto (0), igualando de esta manera cada factor a cero, (px+q=0) o (rx+s=0) y de esta manera encontrar las soluciones.
- Si la ecuación poseen la forma x² + bx + c =0, se debe buscar un numero que sumen b y multipliquen c.
Se debe tener presenta que la gran importancia de las ecuaciones de segundo grado es que pueden resolver y moldear una gran variedad de problemas. Esto en distintas áreas como la ingeniería, biología, economía, física, finanzas, entre otras. La utilización de estas ecuaciones permiten calcular fácilmente el crecimiento de los mercados, el calculo de áreas, la trayectoria de proyectiles y hasta la optimización de costos.









