Los cuadrados perfectos son números que resultan de multiplicar un número entero. Es el producto de un número elevado al cuadrado, el 4 que es el resultado de 2×2 o 16, que proviene de 4×4. Estos números tienen la particularidad de que su raíz cuadrada es exacta y corresponde siempre a un número entero. Lo que los hace fundamentales en matemáticas para resolver problemas relacionados con áreas y proporciones.
Historia de los cuadrados perfectos
La historia de los números perfectos forma parte de una de las más antiguas y fascinantes ramas de las matemáticas: la teoría de los números, desde Babilonia (alrededor de 1800 a.C.), hasta Egipto en el estudio de los cuadrados perfectos. Unos de los primeros en referirse a ellos fue nada menos que Euclides, en su influyente obra (Los elementos), publicada en el año 300 a.C. Había descubierto cuatro números perfectos y en su libro revelaba una forma segura de hallar otros.
¿Cuántos números del 1 al 100 son cuadrados perfectos?
Un cuadrado perfecto es un número tal cuya raíz cuadrada es un número natural. Podemos afirmar que 100 es el cuadrado de 10, es un cuadrado perfecto. Que hay en este rango son los de todos los números naturales menores o iguales a 10 cuadrados perfectos.
- Un número es un cuadrado perfecto, es el resultado de elevar un número entero al cuadrado
- Ejemplo: 1² = 1,² = 4,3² = 9, etc.
- Para encontrar cuántos números del 1 al 100 son cuadrados perfectos:
- Buscamos los números cuyo cuadrado esté entre 1 y 100:
- n² ≤100⟹n≤ √100 =10
- Los números enteros que cumplen esta condición son:1,2,3,4,5,6,7,8,9,10.
- Buscamos los números cuyo cuadrado esté entre 1 y 100:
- Calculamos sus cuadrados:
- 1² =1,2 ² =4,3² =9,4² =16,5² =25,6² =36,7² =49,8² =64,9² =81,10² =100
- 10 números cuadrados perfectos entre 1 y 100, que son:1,4,9,16,25,36,49,64,81,100.
- 1² =1,2 ² =4,3² =9,4² =16,5² =25,6² =36,7² =49,8² =64,9² =81,10² =100
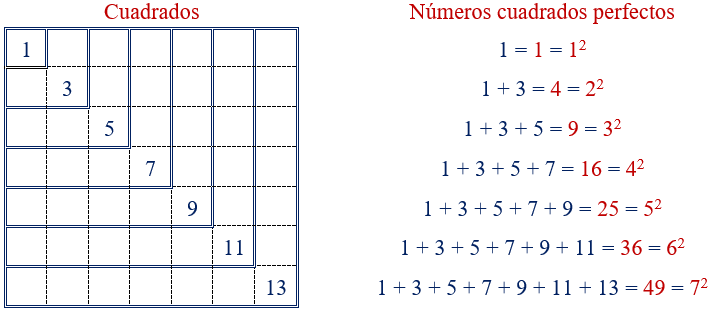
¿Cómo se sacan los cuadrados perfectos?
Los cuadrados perfectos son números enteros que se obtienen al multiplicar un número entero. Para calcular el cuadrado perfecto de un número, simplemente lo elevas al cuadrado, lo multiplicas. Para buscar el cuadrado perfecto de un número más grande o verificar que el número es cuadrado perfecto, se puede usar la raíz cuadrada.
- Pasos para sacar cuadrados perfectos
- Identifica el número: Elige el número entero cuyo cuadrado quieres calcular.
- Multiplícalo: Realiza la operación de multiplicación del número.
- Obtén el resultado: El producto es el cuadrado perfecto.
- Ejemplos:
- 2²=2×2=4 → El cuadrado perfecto de 2 es 4.
- 3²=3×3=9 → El cuadrado perfecto de 3 es 9.
- 4²=4×4=16 → El cuadrado perfecto de 4 es 16.
- 5²=5×5=25 → El cuadrado perfecto de 5 es 25.
- 6²=6×6=36 → El cuadrado perfecto de 6 es 36.
- 7²=7×7=49 → El cuadrado perfecto de 7 es 49.
- 8²=8×8=64 → El cuadrado perfecto de 8 es 64.
- 9²=9×9=81 → El cuadrado perfecto de 9 es 81.
- 10²=10×10=100 → El cuadrado perfecto de 10 es 100.
- 11²=11×11=121 → El cuadrado perfecto de 11 es 121.
- 12²=12×12=144 → El cuadrado perfecto de 12 es 144.
- 15²=15×15=225 → El cuadrado perfecto de 15 es 225.
- 20²=20×20=400 → El cuadrado perfecto de 20 es 400.
- Ejemplos:
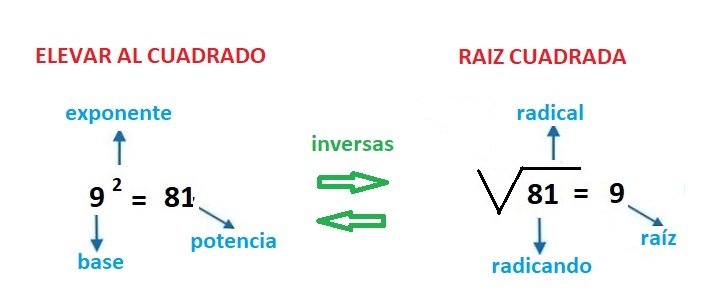
La importancia de los números cuadrados en las matemáticas
Los cuadrados perfectos son más que un concepto abstracto; son una herramienta matemática esencial que conecta múltiples áreas del conocimiento. Tiene aplicaciones prácticas que van desde la educación básica hasta disciplinas avanzadas, la ingeniería y la informática.
- Base en conceptos matemáticos
- Factores primos y raíces cuadradas:
- Los cuadrados perfectos facilitan el cálculo de raíces cuadradas exactas y son esenciales para entender los conceptos de descomposición en factores primos.
- Álgebra:
- Son fundamentales en el desarrollo de identidades algebraicas, el cuadrado de un binomio y la diferencia de cuadrados, esenciales para la simplificación de expresiones.
- Factores primos y raíces cuadradas:
- Geometría y medición
- Áreas cuadradas:
- En geometría, un cuadrado perfecto representan áreas que son útiles en problemas de diseño y construcción.
- Teorema de Pitágoras:
- Este teorema utiliza cuadrados perfectos al relacionar las longitudes de los lados en triángulos rectángulos.
- Áreas cuadradas:
- Aplicaciones en la vida cotidiana
- Optimización de espacios:
- En actividades, el diseño de jardines, suelos y empaques, los cuadrados ayudan a calcular dimensiones óptimas.
- Criptografía y seguridad:
- En ciencias computacionales, los cuadrados juegan un papel crucial en algoritmos criptográficos.
- Optimización de espacios:
- Comprensión y patrones numéricos
- Secuencias y patrones:
- Los cuadrados perfectos son esenciales para analizar patrones numéricos y comprender las propiedades de los números en series matemáticas.
- Desarrollo lógico:
- Resolver problemas que involucran cuadrados perfectos fomenta el pensamiento lógico y crítico.
- Secuencias y patrones:
- Conexión con otros conceptos matemáticos
- Ecuaciones cuadráticas:
- La solución de ecuaciones cuadráticas a menudo implica el uso de cuadrados perfectos.
- Cálculo diferencial e integral:
- En estas áreas, los cuadrados perfectos aparecen en integrales definidas y ecuaciones diferenciales.
- Ecuaciones cuadráticas:
El lenguaje universal de las matemáticas
El álgebra es una rama fundamental de las matemáticas que utiliza letras, números y símbolos para representar relaciones y resolver problemas. Es un lenguaje que permite describir patrones, formular ecuaciones y modelar situaciones del mundo real de manera general y precisa. Dentro del álgebra, el concepto de cuadrado perfecto, es un tema clave que surge al estudiar productos notables. Estos cuadráticos son expresiones que resultan de elevar al cuadrado un binomio. (a+b)² =a² +2ab+b². Este desarrollo muestra que el cuadrado de un binomio genera un trinomio formado con un cuadrado del primer término. El doble producto de ambos términos y el cuadrado del término 2.
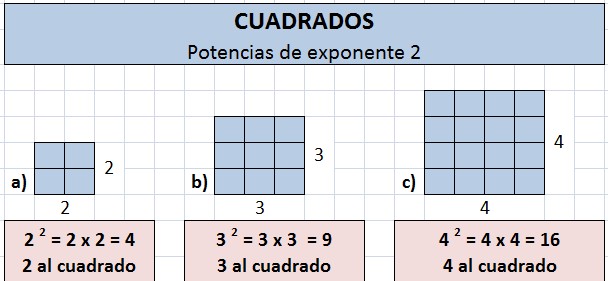
Los cuadrados perfectos son una herramienta esencial en el estudio del álgebra. Esto no solo facilitan la factorización y simplificación de expresiones, ayudan a resolver problemas más complejos en distintas áreas de las matemáticas. Su comprensión es clave para avanzar en temas de las ecuaciones cuadráticas, las raíces y las fórmulas algebraicas. Al dominar este concepto, no solo se mejora el razonamiento lógico, se adquiere una base sólida para enfrentar desafíos matemáticos más avanzados.
