Se puede definir a las cantidades constantes a aquellos valores que NO cambian. Por tanto, se puede asegurar que dichos valores permaneces fijos en un contexto especifico. Se puede tratar de símbolos, números u objetos matemáticos.
Si se toman en cuenta las cantidades variables se puede definir como una diferencia entre ambas que en las variables es posible asumir otros valores. Pero en las constantes el valor se mantiene de manera inalterado.
Algunos ejemplos de las distintas cantidades constantes que podemos encontrar en las matemáticas, son los siguientes:
- Símbolos: Constantes con valor definido, Pi (π) 3.14159265359… o el número de Euler (e) 2.71828.
- Números: Constantes numéricas, 2, 5, -3 o ½.
- Constantes Físicas: Valor fijo en la naturaleza, constante gravitacional (G) o la velocidad de la luz (c).
Contexto de una Constante
Al no poder modificarse el valor de una constante, este depende de la situación o del contexto en el cual se está:
- Si hablamos en le contexto de las matemáticas, la constante es un valor fijo, sin embargo, en ocasiones el valor no está determinado.
- En el álgebra se define a las cantidades constantes como coeficientes de una formula o un monomio.
- Se pueden utilizar las constantes dentro del lenguaje de la programación.
- Dentro de la ciencia, en el área de la física, la constante es la magnitud que no varía en el tiempo.
- Se puede asumir que una función matemática es una función constante si en cada valor de su dominio existe un único valor de su codominio.
- f(x)= 3, en la grafica es una recta paralela al eje Ox.
- En el caso de una ecuación, la constante se refiere al resultado de la misma.
- (x-k) ² + (y-k) ²= 25. En donde x, y son variables, K es un parámetro y 25 es la constante.
La Función de l.as Cantidades Constantes
Se le conoce como función constante aquella función que ignora los argumentos y siempre da el mismo valor. Una función que posee una sola variable, toma el mismo valor ya que no aparece la variable en la expresión de la función.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
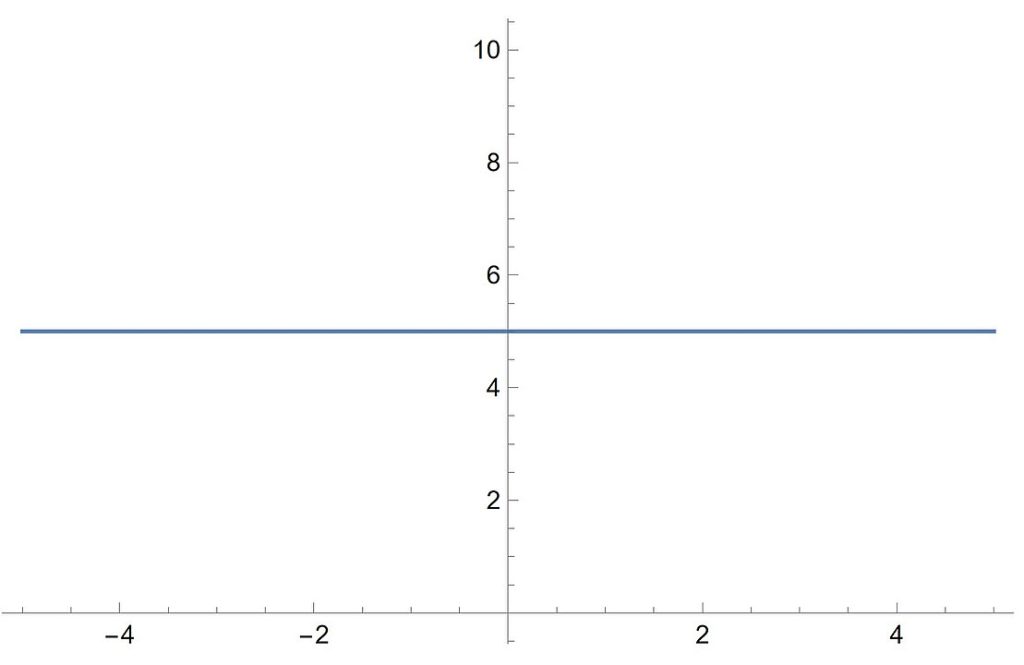
en línea- Ejemplo: f(x)= 5, en su gráfica, la recta es horizontal al eje x.
Dependencia del Contexto de las Cantidades Constantes
En este contexto la palabra “Constante”, significa que la misma no depende de ninguna variable, además NO cambia en el caso de que la variable lo haga. La constante de un contexto estrecho, considera a la variable en un contexto más amplio.

Matemáticas Notables en las Cantidades Constantes
Cuando algunos valores se denotan de manera convencional por un símbolo especifico, se conocen como constantes matemáticas y se identifican con un símbolo especifico.
- Proporcion áurea (φ): equivale aproximadamente 1,6180339887.
- Cero (0).
- Uno (1).
- Pi (π): aproximadamente posee un valor de 3.1415926535 y representa al cociente que existe entre la circunferencia de un circulo y su diametro.
- Raíz Cuadrada de dos (√2): La cual es la longitud de la diagonal perteneciente a un cuadrado de lados iguales y su valor es de 1,4142135623.
- Unidad imaginaria (i ² -1).
- Constante e: con un valor aproximado de 2.7182818284.
- Constante Euler-Mascheroni (y): con un valor aproximado de 0,5772156649.
Constantes en el Campo del Cálculo
En el campo del Cálculo, las cantidades constantes se suele tratar de diferentes formas, ya que por ejemplo la derivada de una constante siempre es 0. Lo anterior se da ya que el valor de la constante no cambia y esta mide la tasa de cambio de la función con relación a la variable.
Por otro lado si se integra la función constante, esta se multiplica por la variable de integración. La constante siempre tendrá el mismo valor antes y después de la evaluación de un limite. Para aquellas operaciones en las que solo se puede diferenciar su resultado por el valor de una constante, se usa la misma derivada.
En otras palabras se debe agregar una constante de integración a una integral indefinida, así se aseguran que se puedan incluir todas las soluciones que existan. Normalmente la constante de integración se identifica con una “c” y significa una constante que posee un valor fijo pero indefinido.
- Ejemplo: Tomando en cuenta que f es una función constante entonces f(x)= 72
F (x)= 0
F(x)dx= 72x+c
Cantidades Constantes que son Variables
Uno de los ejemplos más claros en donde las cantidades constantes pueden ser variables, es dentro del campo de la medicina. Valores como el de la temperatura, pulso, glucosa, los valores de los componentes de la sangre, orina y otras secreciones, pueden variar a través del tiempo. Sin embargo siempre van a tener rangos de normalidad.
Otro ejempl en la programacion y la llamada “Ley de Murphy” (Todo lo que pueda ir mal, ira mal), en donde “Las constantes son siempre variables”. En la programacion ocurre en Pascal, se puede pasar un objeto como parametro a una función.
En resumen lo que debemos recordar y tener presentes que sin importar que las cantidades constantes siempre van a poseer un valor constante. Por lo cual dicho valor no va a cambiar bajo ninguna circunstancia.









