Al contar con tres valores y necesitar un cuarto valor dentro de un problema matemático, en importante aplicar la Regla de Tres y Porcentaje. Dichos valores se establecen proporciones en el agrupamiento de los datos como las cantidades y sus porcentajes.
Es importante repasar los conceptos de la regla de tres, la cual se define como un método matemático en el cual se encuentra una incógnita (un valor desconocido). Se le llama regla de tres ya que nace a partir de tres conocidos.
Esta regla se puede dividir en tres tipos: la Directa (Los valores van en la misma dirección), la Inversa (un valor aumenta y otro disminuye) y la Compuesta (Lleva más de 2 magnitudes y al menos 2 proporciones).
Por su parte el porcentaje se define como aquel símbolo matemático que representa un valor como una fracción dividida en 100 partes. Se puede representar por medio de un porcentaje, una fracción o con el símbolo de porciento (%).
Pasos para la aplicación de la Regla de Tres y Porcentaje
Para aplicar correctamente estos pasos, es importante que se realicen de la manera correcta y sin saltar ninguno de ellos.
- Identificación de datos: Se debe identificar los tres valores conocidos y sus respectivos porcentajes. Importante recordar que el total del porcentaje no debe sobrepasar el 100%.
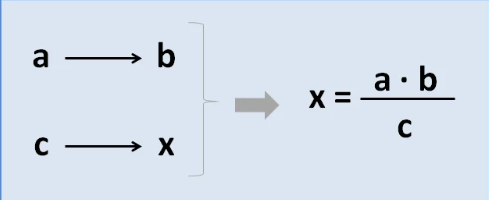
- Proporción: Para plantear la proporción de los valores, se deben crear dos columnas. En una de ellas se pondrán las cantidades, mientras que en la otra los porcentajes. Al valor desconocido se le presenta como el valor “x”.
- Multiplicación: Este paso se lleva a cabo al multiplicar los números de manera diagonal. Esta multiplicación no debe tocar la cantidad en incógnita “x”.
- Dividir: Como ultimo paso se divide el resultado de la multiplicación anterior por el numero “x” o de incógnita.

Ejemplos más Comunes
- Si un camión gasta 10 litros de diesel por cada 100 kilómetros recorridos. ¿Cuántos kilómetros recorrerá el camión con 28 litros de diesel?
Diesel Kilómetros
5 100
28 X
X = 28 x 100 = 560
5
Respuesta: Un camión podría recorrer 560 Km, utilizando 28 litros de diesel.
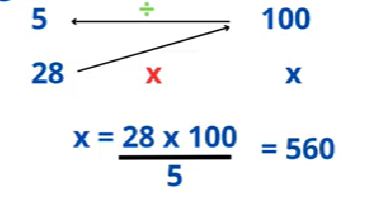
- Sacar el porcentaje de un número. ¿Qué porciento es 30 de 75?
75 100%
30 x%
X= (30 x 100) ÷ 75 = 40%.
- Calculo del porciento de un valor o cantidad. ¿Cuál es el 25% de 150?
150 100
25 x
X = (150 x 25) ÷ 100 = 37.5.
Los Inconvenientes del aplicar la Regla de Tres y Porcentaje
Como en toda regla, siempre se pueden presentar algunos inconvenientes que dificultan la puesta en practica la regla de tres y porcentaje. Comúnmente la regla se puede aplicar en fracciones, pero si estas no son equivalentes, se puede dar que las magnitudes o cantidades no se identifiquen de manera correcta.
Otro inconveniente se puede dar si se aplica la regla sin ningún tipo de criterio en ejemplos o problemas de proporciones inversas. En este caso se podría dar que no se presente una proporcionalidad del todo, complicando un resultado exitoso.
Sin embargo, si en el problema se da la proporcionalidad directa, casi siempre se presentará equivalencia en las fracciones. De esta manera no seria complicado que se de el porcentaje que se necesita en la solución del problema.

Importancia de la Regla de Tres y Porcentaje
Al aplicar la regla de tres y porcentaje su importancia radica en la resolución de problemas profesionales y cotidianos. Ya que por medio de esta aplicación se puede encontrar proporciones desconocidas, facilitando de esta manera diversos cálculos y datos.
Es gracias a la utilización de este método se facilita la resolución de aumentos, descuentos, conversiones de diferentes unidades (recetas, monedas, etc.). De esta manera se convierte en una herramienta esencial en la solución de problemas de manera rápida, y precisa en campos cotidianos como la cocina o profesionales como en finanzas, estadística o lógica.









