Al estudiar más sobre el campo de la geometría en la matemática, se puede identificar sólidos en el entorno y en diversos objetos tridimensionales. Dichos objetos deben tener ancho, largo y alto, además de poseer las características de los solidos (volumen, partículas juntas y ordenadas, forma definida, rigidez e incomprensibilidad).

Dentro de la geometría las figuras que se identifican como solidas son: el cubo, el cilindro, la esfera, el cono y la pirámide. Cada uno de ellos si está en 3D, puede ser identificado fácilmente gracias a ciertas características como, el número de caras, aristas y vértices.

En el caso que la figura se encuentre en 2D las características para su identificación serian las del área, el perímetro, los ángulos, vértices y lados. Cada característica contribuye a identificar solidos en el entorno como en las latas, cajas, pelotas, el cono de helado, entre muchos otros ejemplos que vemos diariamente en la vida diaria.

Las Propiedades para Identificar Solidos en el Entorno

Para identificar correctamente a los solidos dentro de la geometría es importante como primer punto saber diferenciar si la figura se encuentra en 2D (planas) o en 3D (tridimensional).  Para ello cada una de las propiedades brindan los parámetros de reconocimiento.

• Figuras Planas o 2D.
  • Área: Se refiere al espacio que esta dentro del contorno de la figura en cuestión.
  • Perímetro: Es la medida de la línea que se encuentra en el borde de la figura.
  • Lados: Son los segmentos del contorno o líneas de la figura.
  • Vértices: Son aquellos puntos en donde se unen las líneas o lados.
• Ángulos: Es la medida existente entre dos lados que están unidos en un vértice.

• Figuras Tridimensionales o 3D.
  • Vértices: Se refiere a los puntos en donde se unen dos o más lados.
  • Caras: Son aquellas superficies planas que dan forma a la figura geométrica.
  • Aristas: Se le llama de esta manera a las líneas rectas en donde se unen dos caras.

Otras Propiedades

• Interior, exterior y límite: Cada una de las figuras ocupan un lugar en el espacio. Por lo tanto, se define el interior como el espacio interno de la figura, el exterior es el espacio que esta fuera de ella y el límite son las líneas que dividen ambos espacios.
• Similitud y congruencia: Al hablar de similitud se refiere a dos o más figura que comparten la forma pero que pueden tener tamaños diferentes. Por otro lado, nos referimos a congruencia cuando las figuras son exactamente iguales.

Como se identificar sólidos en el entorno

1. Observación: Se debe visualizar la figura de manera general y definir las propiedades que están a plena vista.
2. Cantidad de caras: Al tener una visualización completa de la figura se debe contar cada una de las caras. Por ejemplo, un cubo tiene 6 caras.
3. Visualizar los vértices: Se deben contar los vértices, los cuales unen las aristas. La cantidad de vértices esta unida a la figura geométrica. Ejemplo un prisma posee 8 vértices.
4. Total, de Aristas: Al tener presente de que figura geométrica se esta hablando, se deben contar las aristas que posea dicha figura. Ejemplo el cubo tiene 12 aristas.
5. Clasificación: Tomando en cuenta todos los puntos anteriores y reuniendo la información se podrá llegar a identificar de que figura geométrica se está tratando. Ejemplo, si tenemos dos bases circulares es un cilindro.

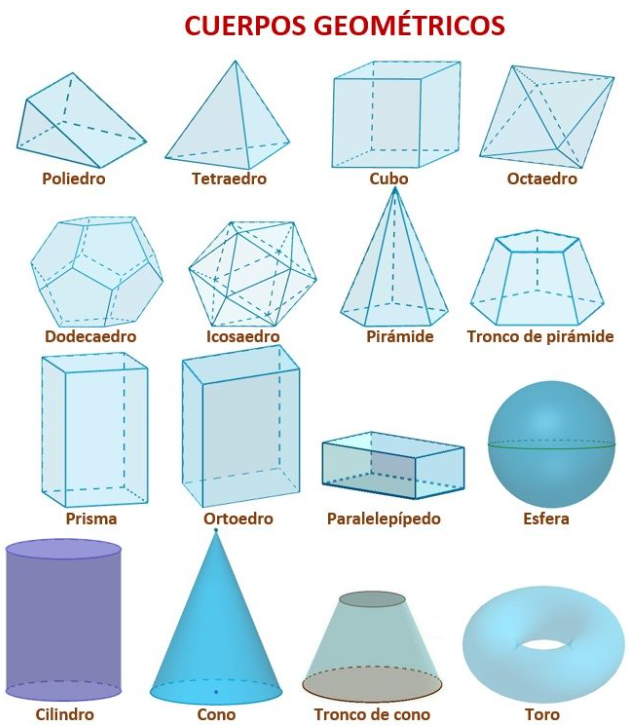
Tipos Comunes de Sólidos

• Cilindro: Posee dos bases circulares y también una superficie en forma de curva.
  • Ejemplo: Un rollo de papel higiénico, una lata, una batería, un vaso.
• Esfera: Es aquella figura que tiene una figura perfectamente redonda.
  • Ejemplo: Una bola, una canica, una naranja.
• Cubo: Esta figura tiene 6 caras iguales y cuadradas.
  • Ejemplo: Una caja de cartón, un cubo Rubik, un dado.
• Prisma: Su forma tiene dos bases iguales y sus caras laterales pueden ser rectangulares o cuadradas.
  • Ejemplo: Si es triangular hablamos de un techo. Mientras que si es rectangular se habla de un ladrillo o un libro.
• Cono: Se forma de una base circular y una superficie que se estrecha hasta convertirse en un punto o vértice.
  • Ejemplo: Un cono de tráfico, un cono de helados o un gorro de fiesta.
• Pirámide: Posee una base cuadrada y caras laterales en forma de triangulo que se unen en un vértice.
  • Ejemplo: Las pirámides.

Importancia de Identificar Solidos en el Entorno

El poder identificar solidos en el entorno es fundamental para el desarrollo práctico y cognitivo. Así como en la gestión ambiental, principalmente en el manejo de residuos mediante el reciclaje durante su clasificación y tratamiento.

Permiten adicionalmente desarrollar una comprensión espacial y fortalecer la habilidad de creación e identificación de figuras tanto en problemas matemáticos como en la vida real. Todo esto en campos como la arquitectura o en el diseño de nuevos productos.