A una porción que se expresa como una fracción, “por cada 100” o de 100 se le conoce como “Porcentaje”. Comúnmente se utiliza para expresar las relaciones entre cantidades de forma clara, si estas están expresadas en facciones. Además, un porciento es posible expresarlo como una fracción si su denominador es 100, en decimales y como un numero entero siempre que se utilice el signo (%) al final.
Para que quede un poco más claro, un porciento es el equivalente a una cantidad dividida en 100 partes, cada una de esas partes corresponde a un 1%. Para expresar un todo de una cantidad se dice que abarca un 100% ósea la cantidad completa del objeto o cantidad.
Cuando se desea identificar claramente un porcentaje, la cantidad debe llevar el signo (%), el cual es llamado “por ciento” o “por cada cien”. Un ejemplo claro de como expresar estas cantidades es, cuando se necesito el 30% de 450, por lo que multiplicas 30 x 450. El resultado se divide entre 100, lo que es igual a 135, por lo que el 30% de 450 = 135.
El Símbolo del Por Ciento

Muchos siempre han identificado el símbolo de porcentaje como %, pero cabe aclarar este símbolo como tal fue impuesto hasta en el siglo XVIII. Entes de él existieron dos versiones, que fueron utilizadas cada una de ellas por hasta un siglo.
Al instaurarse el porcentaje como un tipo de medida se le llamo “per cento”. Por lo que le fue asignado en 1425 un símbolo que consistía en una P (abreviatura de per) acostada sobre la palabra “cento”. Para 1650 el signo evoluciono en una P acostada y en lugar de la palabra cento se cambia por una “o” y un menos (-o).
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea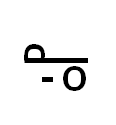
Ya para el siglo XVIII, se inicia a utilizar el símbolo que hasta el día de hoy se utiliza. El cual es una representación de una fracción y en el lugar del numerador y el denominador se pone una “0” separados por una barra inclinada (%).
Origen del Porcentaje
Se tienen datos de su uso pen el siglo XV, en donde se utilizaba para el cálculo de los impuestos o de los intereses de los préstamos. Se cree que su uso proviene del antiguo imperio romano, en la época del emperador Augusto quien estableció el sistema de impuestos.
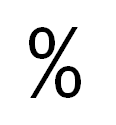
Este sistema establecía que cada persona debía pagar el 1/100, sobre cada artículo, o bien vendido durante la subasta o en los mercados. Se establecía de esta manera ya que con la fracción se podía facilitar el cálculo de los ingresos y estableciendo el denominador de 100 como un estándar.
El llamado “por ciento” nace de la necesidad de simplificar el uso de las fracciones en la vida común, ya que no todos podían realizar cálculos de fracciones complejas. Progresivamente el porcentaje se volvió de uso más común.
Por tanto, se le asigno un signo para acortar aún más su abreviación en el uso continuo. El primer signo nace en 1425 y fue evolucionando hasta llegar al que conocemos hoy en día.
Representaciones del Porcentaje
El porcentaje puede ser representado por medio de fracciones que es como inicio su uso, por medio de números enteros y de decimales. En cada uno de ellos con una fácil operación se puede pasar de uno a otro de manera rápida. Cabe destacar que se pueden utilizar las tres representaciones a la hora de realizar la conversión.

- Fracciones: Se inicia como una tabla de equivalencias en donde el 1% representa a la fracción de 1/100 y esta se va fragmentando hasta llegar al 1/1 que equivaldría al 100%.
- Decimales y Números Enteros: Básicamente esto depende de la cantidad que estemos utilizando como base para realizar la conversión.
- 10% = 10/100 = 1/10=0,1
- 10% de 1000 = 1000/100 = 10 x 10= 100. (el 10% de 1000 son 100).
Ejemplos de la Utilización del Porcentaje
- Ejemplo 1: Si necesitamos saber el porcentaje real del uso de los navegadores web entre los años de 2009 a 2012. Se suman todas las entradas a los navegadores y se toman como un 100%, posteriormente se separan por el tipo de navegador usado hasta dar el porcentaje deseado.
- Ejemplo 2: Si en una escuela hay 500 alumnos y se dice que el 50% son Varones y el otro 50% son mujeres. Eso equivaldría a que 250 alumnos son hombres y 250 son mujeres.
- Ejemplo 3: Si el valor del euro aumenta 0,15 € sobre el valor anterior de 2,50€, lo que equivaldría en fracción a 0,15/2,50= 0,06. Lo que en por ciento seria un aumento del 6%.
El porcentaje presenta su importancia ya que permite expresar de una manera más clara y concisa las relaciones u porciones de un total. Facilitando de esta forma el entendimiento y el análisis de los datos en áreas como las finanzas, contabilidad, negocios, ciencias y en uso diario. Es por esto que actualmente representa una habilidad esencial dentro del gran mundo de las matemáticas.









