En el área del álgebra se conoce como “Escalas “o “Escalamiento” a la multiplicación de las dimensiones que puede tener un objeto. Dicha medida se convierte en un factor a escala, lo que permite lograr una versión mayor o menor de la medida del objeto original. Estas medidas siempre estarán en concordancia con las proporciones originales, ya sea para aumentar o disminuir el objeto en cuestión.
Por lo general las escalas son aplicables en áreas de la matemática como la geometría en la creación de diversas figuras. La cartografía es otra área en donde se encarga de realizar mapas, de igual manera que hoy en día los utiliza la arquitectura en sus planos o maquetas.
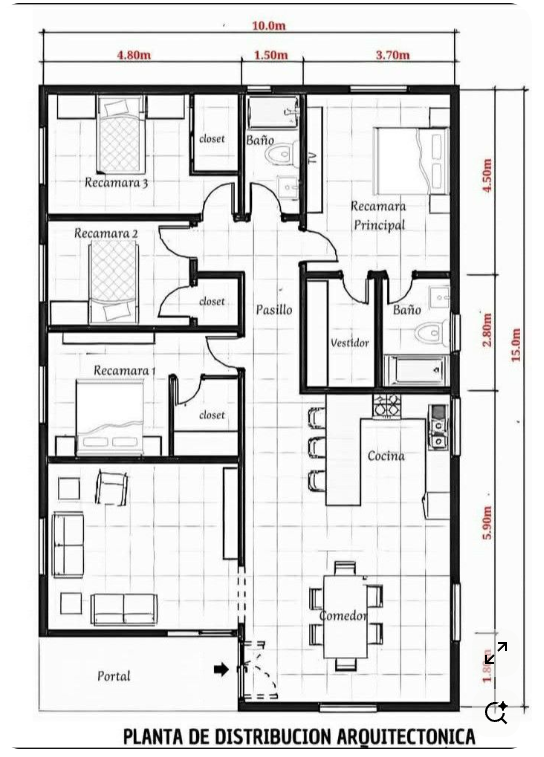
Un ejemplo es un plano a escala de 1:50, representa que por cada metro real de la medida de l objeto base, en este caso una casa, su medida en el plano es 50 veces menor. Esta escala se puede utilizar para aumentar o reducir los objetos y plasmarlos en una maqueta, plano, croquis, etc.
El Factor de una Escala
Para realizar la medición de las escalas, se hace el cálculo de la razón entre la medida que existe entre la figura original y la figura reducida o aumentada. Puede ser utilizada en la medida de volumen, longitud o área.
Cuando obtenemos un factor con una escala mayor a 1, la figura corresponde a una ampliación, mientras que si el factor esta en 0 y 1 corresponde a una reducción. Por otro lado, si el factor corresponde a 1, las medidas son iguales a la del objeto original.
- 2:1, significa que el dibujo es 2 veces mayor al dibujo original.
- 1:1, el dibujo posee la misma medida al original.
- 1:50, corresponde a una reducción y el dibujo es 50 veces menor al original.
Forma de Calcular las Escalas
- Se debe determinar de manera precisa las medidas de la figura original que se va a utilizar, ya esta se utilizara en la multiplicación del factor de escala.
- Seguidamente se escoge si se necesita una ampliación o una reducción de la figura original y cuantas veces de se debe aumentar o reducir estas medidas.
- Tomando esto en cuenta se realizan las nuevas medidas y se indica el tipo de escala que se usó. Para que se tenga una noción de las nuevas medidas, en relación de las originales.
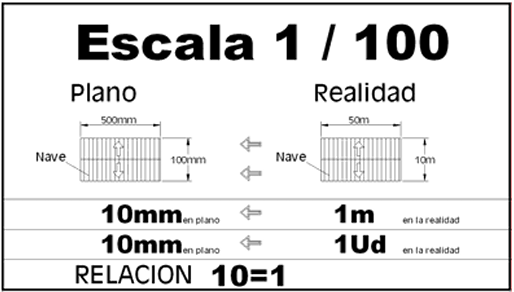
Aplicaciones y Ejemplos de las Escalas
Las escalas pueden ser utilizadas en varias áreas:
- Cartografía: Usado en los mapas que utilizamos diariamente, ya sea los que representan un país, un continente o todo el planeta. En esta área la relación que existen entre las distancias que se pueden ver en los mapas y sus distancias reales. Por lo general son utilizados para representar grandes territorios.
- Matemáticas: Es aplicable a diversas figuras similares, cuya escala es mayor o menor a 1. Se utiliza en las representaciones graficas en áreas como geometría, algebra, funciones, entre otras.
- Arquitectura e Ingeniería: Usada para representar edificios, casas, complejos residenciales o cualquier tipo de construcción en diferentes tipos de relieve. Su representación puede ser por medio de croquis, planos o maquetas.
Representación General de las Escalas
Un objeto o representación puede tener varios tipos de escalas al mismo tiempo, las cuales dependen directamente de las necesidades de quien las elabora y el para que se elabora. Un ejemplo de esto es el proyecto de construcción de una carretera, en la que se pueden presentar escalas verticales u horizontales. También puede presentar maquetas del relieve y los planos de su trayecto y construcción.
Otro ejemplo es el de la construcción de un puente, en donde se necesitan escalas del relieve que lo rodea. La dirección del viento de manera dimensional y su efecto sobre la estructura, así como representaciones en maquetas, planos.
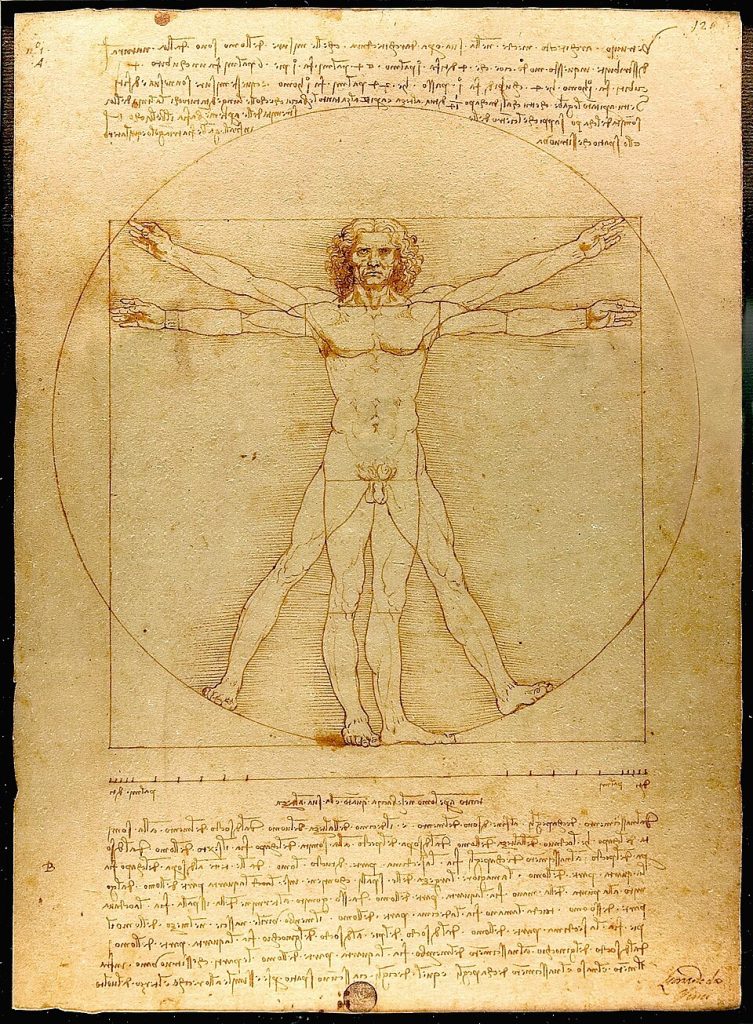
Quizá uno de los más conocidos es la ilustración de Leonardo Da Vinci, el cual se conoce como el “Hombre del Vitruvio”. Dicha imagen representa el cuerpo humano y sus debidas proporciones que se denotan en una escala casi exacta. De la misma manera en que se ilustran los dibujos en planos de ingeniería y arquitectónica.
Las escalas son altamente funcionales en la representación de proporciones reales, aumentadas y disminuidas en una dimensión lineal de un modelo determinado. Pueden ser representadas por medio de palabras, fracción, grafica y como una constante. Su fácil visualización contribuye a una imagen general de todo un proyecto, problema o ecuación.
