En el área de las matemáticas una relación de dependencia, habla de la conexión que existe entre dos conjuntos de elementos. En los que el valor de un elemento (variable dependiente), depende directamente del valor del otro elemento (variable independiente).

Sin embargo, el cambio en una variable cambia con respecto al cambio de la otra parte que la conforma. De esta manera se crea una parte independiente y una que depende de la primera. La parte independiente es aquella que puede cambiar o ser manipulada, ya que su valor no depende de ninguna variable en la relación.

Comúnmente a la parte variable independiente se le asigna la letra “x”. Por otra parte, la variable dependiente esta directamente relacionada a su contraparte (independiente) y su valor puede cambiar si el valor de la variable independiente lo hace. Por lo general es representada con una “y”.

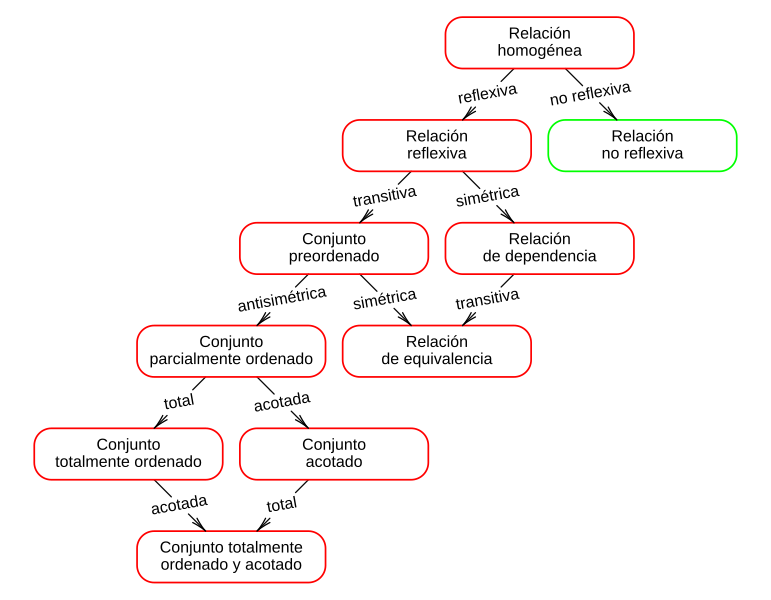
Ejemplo de Variable Independiente y Dependiente

Si tomamos una función simple matemática y=2x+1.

• Variable independiente: x (su valor puede cambiar)
• Variable dependiente: y (su valor depende del valor de “x” que escojan).

X= 3, por tanto y=2(3) +1=7.

X= 2, entonces y=2(2) +1=5.

Por tanto, si se cambia el valor de “x”, el valor de “y” también cambiara como consecuencia debido a la relación de dependencia. Ya que esta describe como un valor es directamente dependiente o influenciado por otro valor (independiente).

Tipos de dependencia

• Funcional: Se refiere a una dependencia cuya variable es una función de otra. Por ejemplo y=2x+3, en donde “y” depende de “x”.
  • Ejemplo: El circuito eléctrico, en donde la corriente (l) es la función del voltaje (V), la resistencia (R), de acuerdo a la Ley de Ohm, donde l=V/R.
• Lineal: El conjunto de vectores lineales es dependiente si uno logra expresarse en una combinación lineal de los demás.
  • Ejemplo: Si un vector se escribe como una combinación de otros, quiere decir que son lineales dependientes.
• Estadística: En ellas las variables están relacionadas, sin embargo, no de forma exacta.
  • Ejemplo: Se usa la relación entre la cantidad de horas de estudio y la calificación final del examen.

Las dependencias pueden se estadísticas, lineales o funcionales y cada una de ellas tiene una manera diferente de interactuar con las variables.

Teorema de Dependencia Funcional

Se refiere a un tipo de dependencia funcional que es una generalización de una dependencia lineal. Se indica que son funcionalmente dependientes si en un conjunto existe una relación funcional entre ellas. También se establece que una aplicación de este teorema es que con las condiciones adecuadas una función que dependen de “n” parámetros, se pueden expresar como una función de conjunto de variables.

También establece que en una condición necesaria di las funciones son de clase C, los menores de la matriz jacobiana. Son idénticos a nulos o equivalentes a un rango menor a “m”.

Ejemplos de Relaciones de Dependencias

• Ejemplo 1:
  • En un conjunto finito A, conformado por el elemento A= {a,b,c} y se defina la relación binaria R, de manera que R= {a,b} x {a,b} ꓴ {a,c} x {a,c}. De manera extensiva se vería así: R={(a,a), (a,b), (b,a), (b,b), (a,c), (c,a), (c,c)}.

• Ejemplo 2:
  • En un mapa plano “M” y tomando en consideración las diversas superficies, en las que el plano es dividido. Se podría estableces como superficies colindantes que comparten un linde.
  • Si dos superficies colindan, se puede pasar de una a otra, sin la necesidad se pasar por una tercera. Se puede representar que “x” y “y” son colindantes de la siguiente manera x,y Є M: C(x,y).

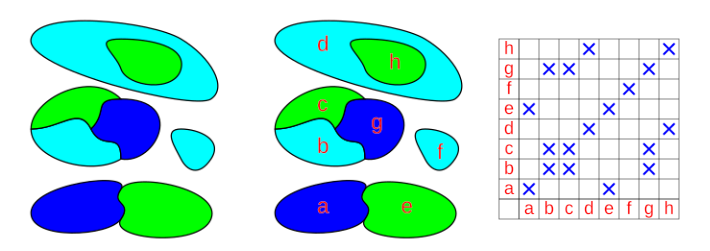
En una unidad binaria que es colindante como M se debe cumplir con las siguientes propiedades:

1. Es reflexiva ꓯxЄM : C(x,x).
2. Si en la superficie del mapa “x”, se puede pasar de una de esas superficies a otra sin llegar a una tercera, siendo simétrica: ꓯx,yЄM : C(x,y)          C (y,x).
3. Si “x” colinda con “y”, entonces “y” es colindante con “x”.
4. Una relación de dependencia es una relación binaria colindante si además son simétricas y reflexiva.
5. La propiedad transitiva no cumple con una relación colindante cuando: ꓯx,y,zЄM : (C(x,y) Ʌ C(y,z))              C(x,z).
6. Si “x”, “y” y “z”, se cumple que “x” colinda con “y” y “y” es colindante con “z”, no significa que “x” es colindante de “z”. Lo que significa que la propiedad transitiva no se cumple y por tanto la relación colindante no es equivalente.

La dependencia matemática se refiere a un conjunto o una variable que se pueden relacionar con otras. También se puede indicar que un valor puede determinar el valor de otro por medio de una estadística o probabilidad.