Dentro de la matemática, tanto el álgebra como las relaciones, poseen una relación muy estrecha e intrínseca. Mientras que el álgebra puede proporcionar técnicas y herramientas para analizar y representar relaciones existentes entre las cantidades. Las relaciones representan al objeto de estudio del álgebra.

Se podría describir a la relación, como aquello que conecta los elementos matemáticos de uno o varios conjuntos. Uno de los ejemplos más comunes es el del par ordenado (x, y), donde “x” forma parte de un conjunto y la “y” pertenece a otro conjunto.

En términos simples, la conjunción entre las relaciones y el álgebra lo que busca es generar una fácil comprensión de los patrones matemáticos. De esta manera empezar a leer y escribir (manipular) los símbolos básicos en las operaciones e identificar su ubicación dentro de la recta numérica.

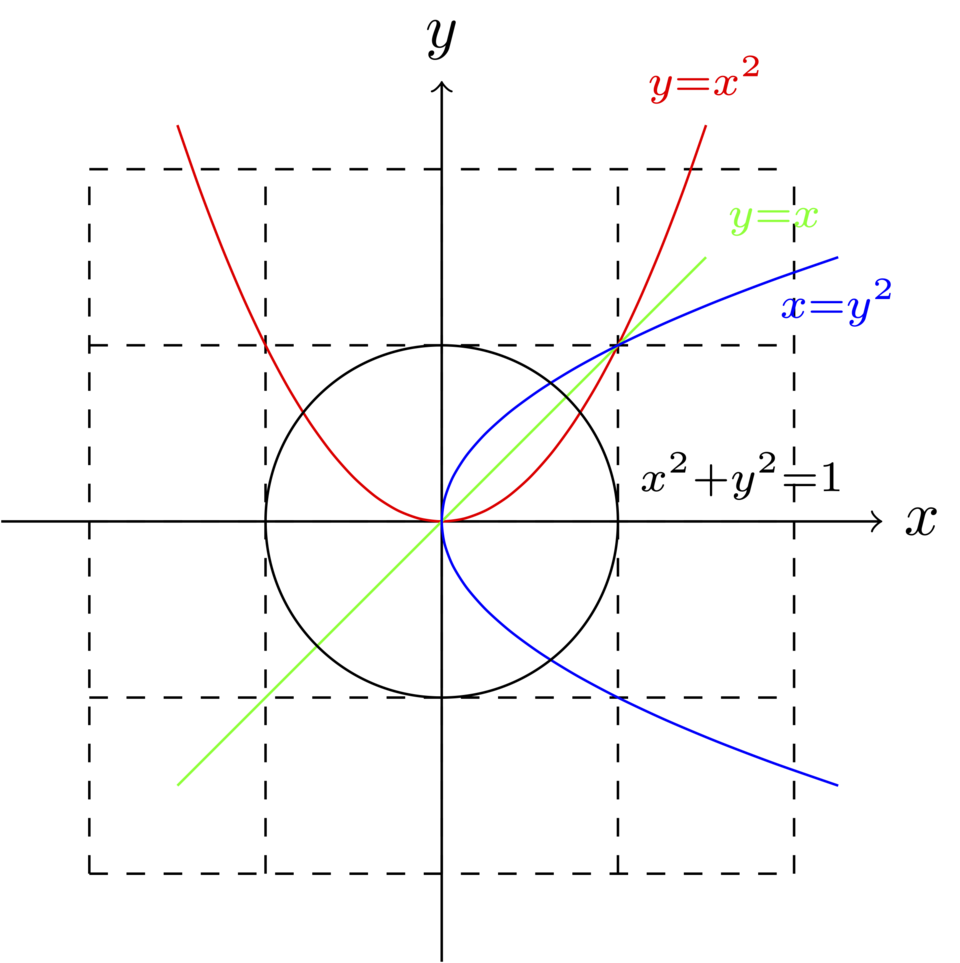
Tipos de Relaciones

Las relaciones algebraicas se pueden clasificar de acuerdo a sus distintas propiedades. Adicionalmente existen gran variedad de tipos, sin embargo, les presentamos a continuación las principales:

• Relación Vacía: Indica que ningún elemento, perteneciente a un conjunto tiene relación con otro, ni consigo mismo.
• Relación Universal: En este se indica que todos los elementos pertenecientes a un conjunto poseen relación con los demás elementos del mismo conjunto o con otros elementos.
• Relación Reflexiva: Sus elementos posee una relación consigo mismo y con otros.
• Relación Transitiva: Un elemento se puede relacionar con otro elemento y este a su vez con otro. Hasta que el ultimo se relacione con el primero.
• Relación de Identidad: Indica que cada uno de los elementos que pertenecen a un conjunto se relacionan consigo mismo.
• Relación de Equivalencia: Este tipo derelación indica que puede ser simétrica, reflexiva y transitiva al mismo tiempo.
• Relación Simétrica: Hace referencia a que, si un elemento se relaciona con otro, entonces este se relaciona con el primero.
• Relación Antisimétrica: Se dice que dos elementos son iguales si, el primero se relaciona con el segundo y viceversa.
• Relación Inversa: Se obtiene al invertir las parejas reunidas u ordenadas de una relación original.

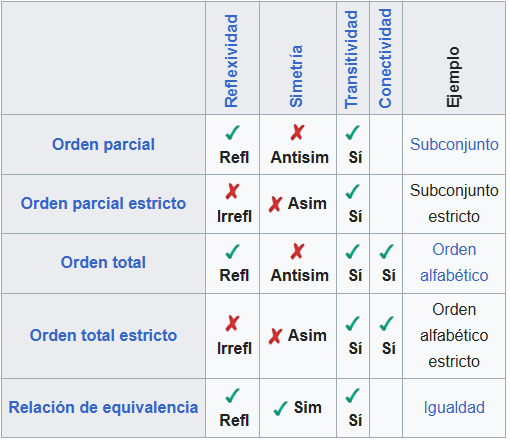
Combinaciones de Propiedades

Cuando las relaciones satisfacen algunas combinaciones de sus propiedades (anteriormente nombradas), se les puede otorgar nombres propios:

• Orden Parcial: Obedece aquellas relaciones que son reflexivas, transitivas y antisimétricas.
• Orden Total: Pueden ser relaciones antisimétricas, transitivas, conexas y reflexivas.
• Orden Parcial Etricto: Se identifican con las irreflexivas, transitivas y antisimétricos.
• Orden Total Estricto: Son aquellas que son antisimétricas, conexas, transitivas y irreflexiva.

Representaciones de una Relación

Las diferentes relaciones pueden ser representadas de diferentes maneras como las siguientes:

• Tablas: Son usadas para demostrar la relación entre los elementos de dos conjuntos. Cada una de sus filas puede representar un par ordenado.
• Pares Ordenados: Expresan pares como (x, y), en donde la “x” se encuentra en un conjunto de partida y la “y” a uno de llegada.
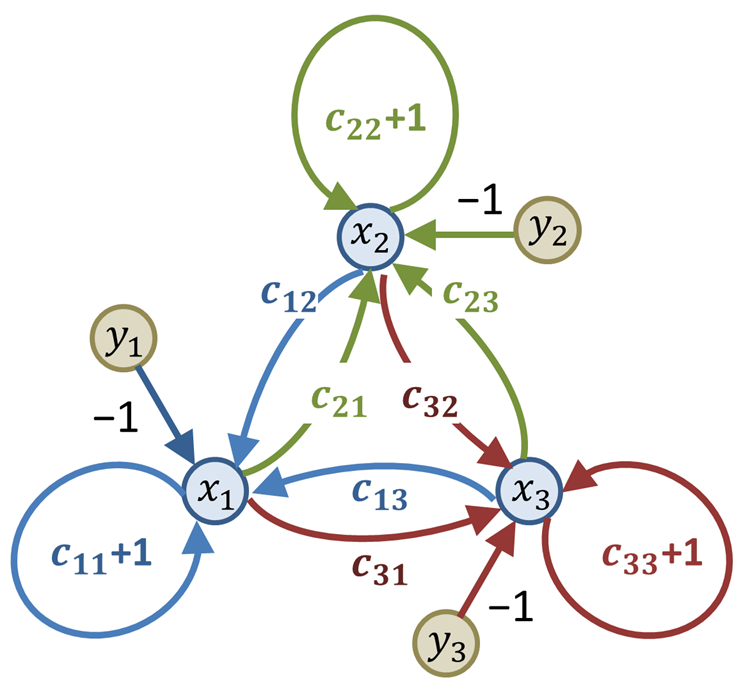
• Matrices: Dentro del algebra lineal, se usan las matrices como modo de representación de las relaciones binarias, como en conjuntos finitos.
• Diagramas de Flechas: Se usan flechas dentro de los conjuntos de elementos, para poder visualizar la correspondencia existente entre ellos.
• Gráficas: Por medio de las coordenadas cartesianas, una relación se puede ver representada entre un conjunto de puntos o como una curva.

Teoremas de las Relaciones

Dentro de las relaciones se pueden dar pautas que al cumplirse a cabalidad se pueden definir como teoremas. Ya que estos son las afirmaciones que pueden ser demostrados a través del razonamiento matemático, lógico o deductivo.

• Cuando una relación es reflexiva debe si o si ser su complemento irreflexivo.
• Una relación es asimétrica solo si es irreflexiva y antisimétrica.
• Si una relación es inversa solo si es también simétrica.
• Se considera una relación transitiva e irreflexiva solo si es asimétrica.
• Una relación puede ser conexa solo si el complemento es asimétrico.
• Si una relación es fuertemente conexa, también debe ser reflexiva y conexa.
• Una relación es fuertemente conexa su complemento debe ser asimétrico.
• Si una relación es irreflexiva, reflexiva, asimétrica, simétrica, antisimétrica, conexa, transitiva y fuertemente conexa, su reciproca debe serlo de igual manera.
• Si por ejemplo tenemos una relación R y esta esta contenida en una relación S, estas deben:
  • Si R es: fuertemente conexa, reflexiva o conexa, en total por la derecha o izquierda, entonces la relación S también lo es.
  • Si S es: asimétrica, irreflexiva y antisimétrica, única por derecha e izquierda, entonces R también lo es.

Importancia de las Relaciones

Dentro del álgebra, la importancia de las relaciones radica en la capacidad para poder moldear las conexiones entre los diferentes conjuntos y elementos. Estas relaciones permiten resolver los diferentes problemas matemáticos aplicados a diferentes áreas. La informática, la economía, la ingeniería y la física, son solo algunos ejemplos de áreas que utilizan deferentes tipos de relaciones.

En esencia una relación se puede describir como la conexión que existe entre dos o más objetos, que a menudo se representan como pares ordenados. En resumen, cada elemento de un conjunto denominado dominio, le corresponde igualmente otro elemento de otro conjunto denominado rango.