Para poder establecer relaciones entre operaciones se debe entender que dichas conexiones se dan entre las operaciones entre conjuntos y el orden de las operaciones. El primer concepto se refiere a los elementos como la unión, diferencia, intersección y complemento.
Mientras que al hablar del orden de las operaciones se refiere al PEMDAS, el cual sugiere el orden en el cual se deben realizar las operaciones matemáticas para su solución. Ambos métodos permiten comparar y combinar diferentes grupos de elementos.
Dentro del grupo de las relaciones entre operaciones también se encuentran las relaciones de orden las cuales incluyen las comparaciones de mayor que (>), menor que (<) e igual que (=). Esta relación permite la comparación de las cantidades.
Tipos de Relaciones
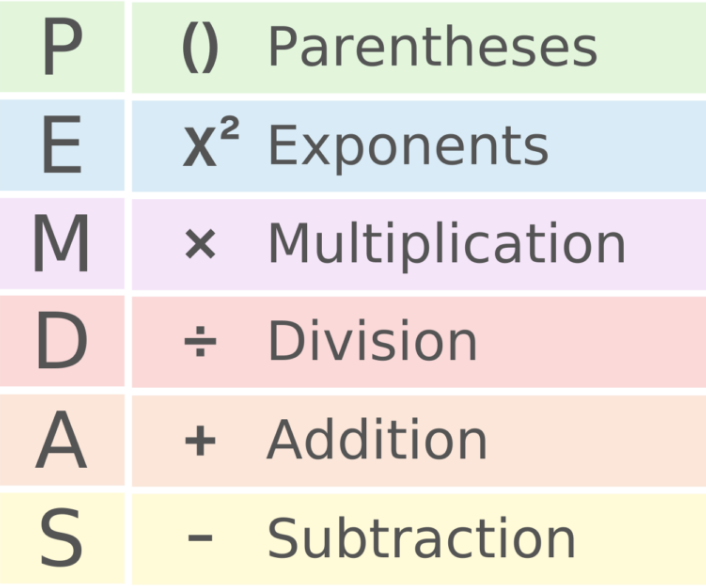
- Jerarquía de las Operaciones: Se refiere al orden que se les da a las operaciones para lograr una correcta solución. También es conocido por las siglas PEMDAS (Paréntesis, Exponentes, Multiplicación, División, Adición y Sustracción).
- Paréntesis: Se refiere a las operaciones que se encuentran dentro de los paréntesis, ya sean redondos (), cuadrados [] o corcheas {}. Se inicia por los que estén más adentro y de ahí hacia afuera.
- Exponentes: Se refiere a las operaciones como la raíz (√) y las potencias (x²).
- Multiplicación y División: Se resuelven primero las multiplicaciones, seguidas de las divisiones, las cuales se resuelven de izquierda a derecha.
- Sumas y Restas: Seguido se realizan las sumas, y por ultimo las restas. Igualmente se resuelven de izquierda a derecha.
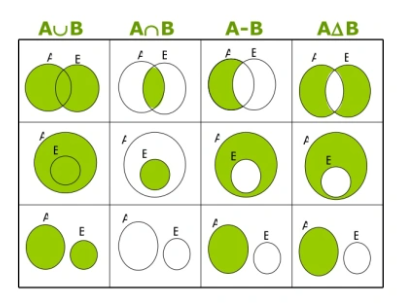
- Operaciones entre Conjuntos: Utilizados para comparar y comparar al menos dos o más conjuntos, esto con el objetivo de formar uno nuevo. En este tipo de operaciones podemos encontrar las de unión (ꓴ), Intersección (ꓵ), Diferencia (-) y Complemento.
- Unión (ꓴ): Son aquellos que combinan dos o mas conjuntos. Ejemplo: (A ꓴ B).
- Intersección (ꓵ): Este conjunto solamente contiene los elementos que son más comunes en ambos conjuntos (A ꓵ B). Ejemplo: {5, 6, 7} y {6, 7, 8} es {6, 7}.
- Diferencia: Son aquellos conjuntos que pueden contener elementos que se encuentran el conjunto A, pero no está en el B (A-B). Ejemplo: A= {2, 3, 4}, B= {4, 5}, por lo tanto, A-B= {2, 3}
- Complemento: Son los conjuntos que pertenecen al conjunto universal (U) pero no se encuentran en el conjunto A.
Relaciones entre Operaciones Lógicas y Funciones
Se refiere a aquellas relaciones entre operaciones que se pueden describir como las que conectan dos o más conjuntos.
- Función: Se refiere a aquellas relaciones en las que cada una de ellas posee una entrada y, en consecuencia, también poseen una salida.
- Relación: Se refiere a la forma de conectar los elementos de un conjunto, los cuales se pueden expresar en pares ordenados (entrada, salida).
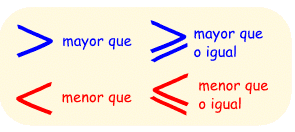
- Relaciones de Orden: Son aquellas que se usan en la comparación entre las cantidades, incluyendo la posibilidad de igualdades numéricas.
- Mayor que (>) y Menor que (<): Utilizadas generalmente para comparar números y determinar cual de ellos es mayor y cual es en consecuencia menor. Ejemplo: 5 > 4 y 4 < 8.
- Mayor o igual que (≥) y Menor o igual que (≤): Permite la comparación de aquellos números en los que se puede incluir una probable igualdad. Ejemplo: Y ≥ X
- Igual que (=): Son aquellas comparaciones en las que ambos números son iguales y por lo tanto no hay uno mayor o menor al otro. Ejemplo: 8 = 8.
Importancia de Establecer relaciones entre operaciones
Al lograr establecer relaciones entre operaciones se permite el análisis y la manipulación de datos de una manera lógica. Obteniendo mayor eficiencia a la ora de resolver problemas en distintas áreas como en programación o dentro de las bases de datos.
Adicionalmente facilita la comprensión de las operaciones elementales o básicas que se pueden relacionar entre sí como la multiplicación con la división o la suma con la resta. Cada conjunto de datos logran una vinculación por medio de las operaciones como la composición, la unión o la intersección.
Es gracias a estas relaciones que se puede dar solución a problemas complejos en campo como la inteligencia artificial (IA), Educación, informática y la big data. Las soluciones obtenidas de estas relaciones entre operaciones permiten soluciones claras y precisas.
