Se define como regla de tres a un tipo de procedimiento matemático usado para resolver los problemas de porcentajes entre magnitudes. Esto quiere decir que, con el conocimiento de tres datos de un problema, se puede conocer un cuarto valor desconocido.
Al aplicar esta regla se logra establecer una relación de proporcionalidad y linealidad, entre los valores. Debido a la facilidad de comprensión y utilización se ha vuelto muy útil en varios tipos de problemas donde existe una incógnita matemática.
Su aplicación se puede usar para ajustar recetas de cocina, comprender los descuentos de las compras o calcular la distancia de un viaje. Recordemos que se puede llegar a conocer el valor de una incógnita, siempre que conozcamos al menos tres datos.
Tipos de Reglas de Tres
Existen dos tipos de regla de tres, las cuales se definen como la Regla de tres simple y la regla de tres compuesta. La Simple se divide a su vez en Directa y Inversa, las cuales explicaremos a continuación:
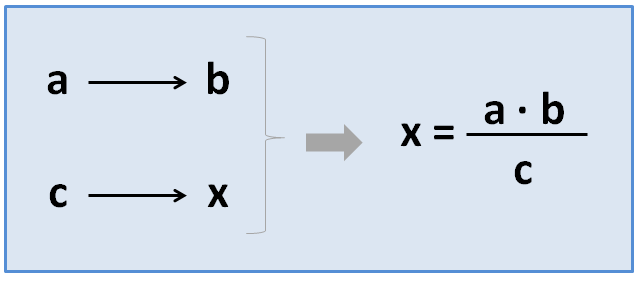
- Regla de Tres Simple: Establece la relación de la proporcionalidad que existe entre 2 valores conocidos (A, B) y un tercer valor como incógnita llamada comúnmente “X”. Con estos tres valores se de calcular un cuarto valor conocido como “Y”.
A→B
X→Y
- Regla de Tres Directa: Cuando las dos magnitudes se comportan de una misma manera. Según lo anterior cuando el valor de A aumente, el valor de B también aumenta, lo que indica una relación de proporcionalidad.
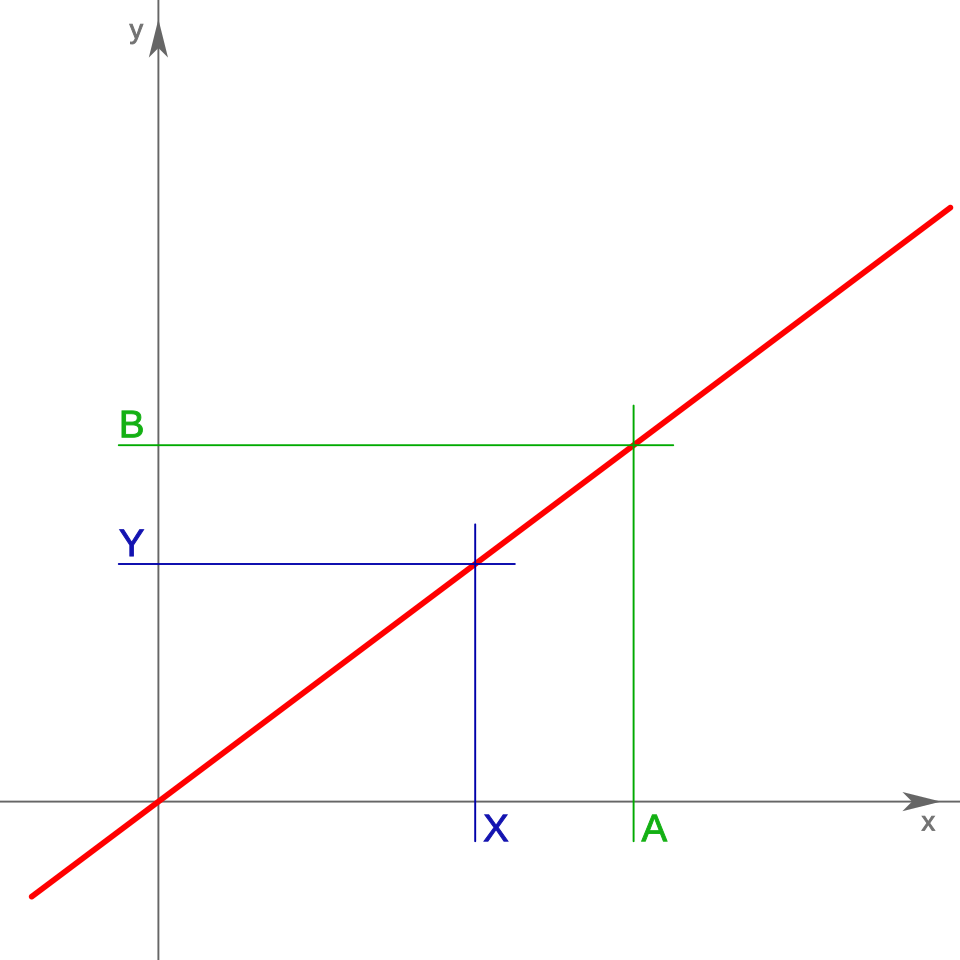
B/A = Y/X = k (cociente de proporcionalidad).
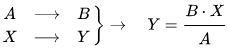
Ejemplo: Si tengo 8 litros de pintura y con ellos pinto 2 habitaciones ¿Cuántos litros necesito para pintar 5 habitaciones?
- Regla de Tres Inversa: Utilizada cuando una de las dos magnitudes crece (A), mientras que la otra decrece (B) en una misma proporción. A*B → X*Y = e (producto constante).
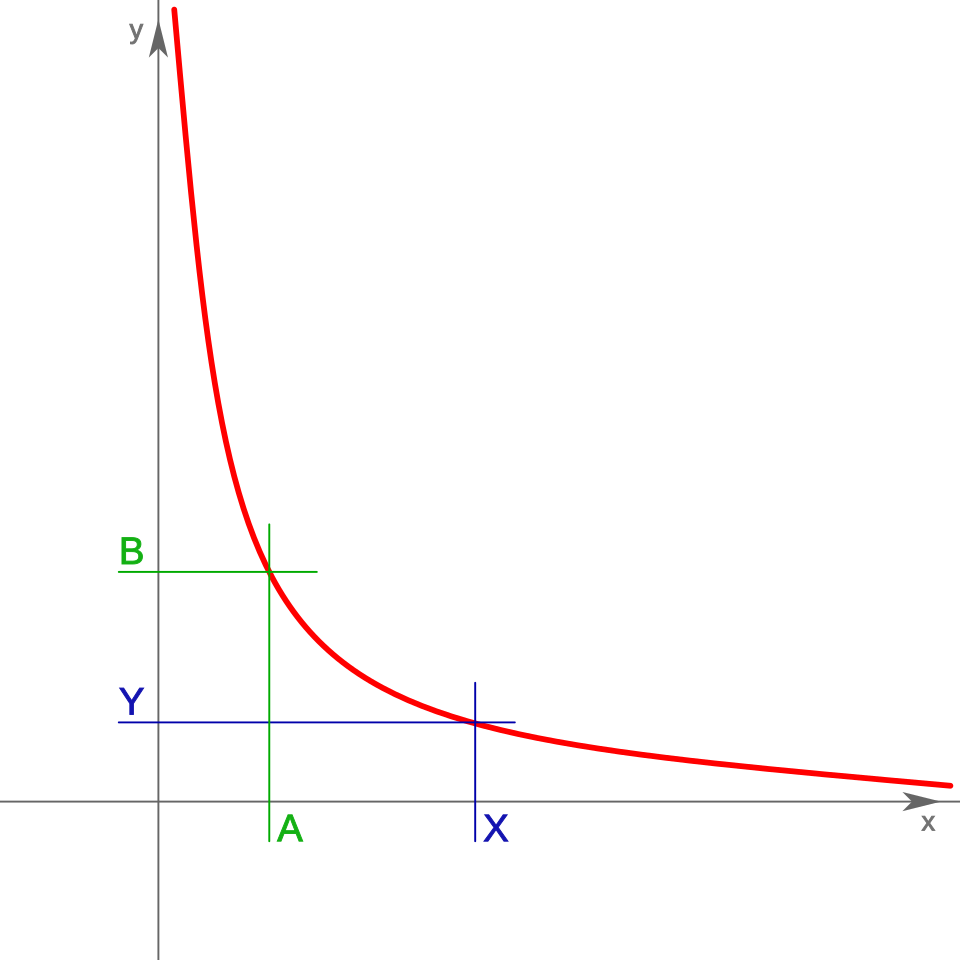
Ejemplo: Si 8 trabajadores duran 15 horas en construir un muro ¿Cuánto tardaran 5 trabajadores en construir el mismo muro?
- Regla de Tres Compuesta: Cuando en un problema participan más de dos magnitudes, se le conoce como compuesta. Ya que el problema plantea más de 3 cantidades conocidas, además de la cantidad en incógnita o desconocida.
- Ejemplo: 12 trabajadores construyen una pared de 100 metros en unas 15 horas ¿Cuántos trabajadores se necesitan si se debe levantar un muro de 75metros en solo 26 horas?
Resolución de la Regla de Tres
Después de conocer los diferentes tipos de reglas de tres, es importante establecer los pasos adecuados para resolver este tipo de problemas.
- Identificación de las magnitudes: Se debe determinar en el problema cuales son las magnitudes (litros, metros, días, etc.) involucradas y su tipo de relación.
- Clasificación de la relación: Se debe establecer si la relación que une a las magnitudes es directa o inversa.
- Organización de los datos: Se debe establecer los datos en una forma tabular, poniendo las magnitudes iguales juntas y debajo de la magnitud correspondiente la incógnita (X).
- Aplicación de la Fórmula: Después de saber que tipo de regla es, se debe aplicar.
- Directa: A=B/C*D.
- Inversa: A=(B*C) /D.
- Calculo del Resultado: Después de realizar la operación se descubre el valor de la incógnita.
Aplicaciones e Importancia
La regla de tres puede ser ampliamente utilizada en diversos campos, los cuales pueden ser usados en la vida cotidiana:
- Adaptar Recetas: Es usado para ajustar las distintas cantidades de los ingredientes necesarios, dependiendo de la cantidad de comensales.
- Cálculo de Consumo: Sirve para determinar la cantidad de gasolina o combustible que se necesita para recorrer una cierta distancia.
- Cálculo de Porcentaje: Utilizado para hallar el valor de un porcentaje que no se conoce.
- Razonamiento Lógico: Ayuda con el desarrollo de habilidades, para prever cuando una magnitud afecta a otra y mejora de esta manera la comprensión de la relación.
- Conversiones: Útil para poder cambiar fácilmente entre diferentes unidades de medición.
En vista de lo estudiado anteriormente, se puede establecer que la regla de tres como una herramienta que se usa en diversos contextos. En los campos profesionales como la nutrición, la ingeniería o el comercio, pueden resolver problemas cotidianos.
