Se define como una proporción directa, cuando dos magnitudes disminuyen o aumentan en la misma proporción juntas. Si una magnitud se llega a dividir o multiplicar por un número, la otra magnitud realizaría la misma operación con el mismo número.
Por tanto, si tomamos ambas magnitudes y las expresamos como una misma constante (k), en donde la variable dependiente (y) sería igual a la variable independiente (x). La cual es multiplicada por esa constante, en otras palabras y=kx.
Con lo anteriormente definido queda claro que dos secuencias de números son directamente proporcionales si cada uno de sus elementos poseen una razón constante. Esta razón obtiene el nombre de “constante de proporcionalidad”, mientras que su reciproco es conocido como “constante de normalización”.
Ambas secuencias pueden ser inversamente proporcionales si los elementos que la forman poseen un producto constante.
Características de la Proporcionalidad Directa
Para entender de una manera más sencilla la proporción directa, es necesario explicar de manera más detenida cada uno de sus características principales:
- Cociente Constante: Corresponde al cociente existente entre las dos cantidades, las cuales deben ser iguales a una constante (k).
- Relación Constante: Se genera cuando, si una cantidad disminuye o aumenta, la otra lo hace de la misma manera.
- Gráfica: Cuando se grafica una relación de proporción directa, se puede obtener una línea recta, la cual pasa por el punto de origen (0,0).
- Formula: Representada como y=kx, en donde la “y” representa a la magnitud dependiente, la “x” es la magnitud independiente y finalmente “k” representa la constante proporcional.
Ejemplos de la proporción Directa
- En la circunferencia de un círculo, el diámetro es proporcional a la constante de proporcionalidad igual a pi (π).
- Si un objeto viaja a una velocidad constante, se puede decir que la distancia que se recorrió es directamente proporcional al tiempo que duro el viaje. De esta manera la constante de proporcionalidad seria la velocidad.
- La distancia que se recorre, suele ser directamente proporcional a la cantidad de gasolina que es consumida por el vehículo. En otras palabras, a más distancia, mayor la cantidad de gasolina que se necesita.
- Si un producto tiene cierto precio por kilo, el precio total que se pague, será directamente proporcional a la cantidad de kilos que compremos de ese producto.
- Si tomamos la fuerza neta que actúa sobre un objeto, se puede indicar que es proporcional a la aceleración, según el sistema de referencia inercial. Esta proporcionalidad se da gracias a la segunda ley de Newton.
Representación de la Proporción Directa
Como se ha indicado anteriormente, para que se pueda dar una proporción directa, se debe crear la relación de y=kx, tomando como base lo siguiente:
- X: Representa a la variable independiente.
- Y: Es la variable dependiente (es directamente proporcional a “x”).
- K: Se denomina como la constante positiva.
Si tenemos que x≠0 se puede expresar a la constancia de proporcionalidad de la siguiente manera: K= y/x. También se le puede denominar como constante de proporcionalidad o constante de variación.
Por tanto, la proporción directa se puede visualizar como una ecuación lineal con dos variables, la cual posee una intersección en “y” de 0 y en la pendiente de k>0, lo que se traduce en un crecimiento lineal.
Importancia de la Proporción Directa
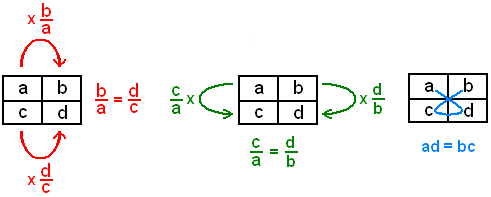
La proporción directa es de gran importancia en la matemática, ya que establece una relación lineal y predecible entre dos magnitudes. Lo que quiere decir que, si una de ellas aumenta, la otra lo hará de la misma manera proporcionalmente, y lo mismo pasará si una cantidad disminuye.
Puede ser expresada como una razón constante (a/b = c/d). Es utilizada constantemente en la resolución de algunos problemas prácticos de la vida cotidiana, en la ingeniería y en la ciencia. Ayuda en la toma de decisiones eficientes e informadas.
