Para comprender la relación de las gráficas de figuras con escala, se requiere poder entender la relación existente entre las matemáticas, el dibujo y la realidad. Esto en base a que la figura se convierte en una de regla graduada para entender a pequeña escala, lo que está en tamaño real.

De una forma más clara se puede definir a una gráfica de figura con escala a una representación fiel y visual de una figura u objeto que se encuentra en tamaño real. Dicha representación se puede presentar por medio de un mapa, plano, dibujo, maqueta, etc. Las medidas de la figura han sido reducidas o aumentadas a en una escala proporcional para mantener la concordancia con el modelo real.

Al establecer una escala clara ya sea para la reducción o aumento de medidas, se permite realizar cálculos y medidas sencillas en el modelo. Esto sin la necesidad de recurrir a instrumentos complicados o a la perdida de tiempo y recursos. Desde un simple plano o maqueta se puede construir un edificio especificando sus medidas reales y su visión total del proyecto.

¿Qué son las Gráficas de Figuras con Escala?

Se le considera como una especie de relación visual existente entre un modelo real, representado en un dibujo, plano o mapa. Sus dimensiones son exactas a las del modelo real, solamente que en una escala menor o mayor según sea la necesidad.

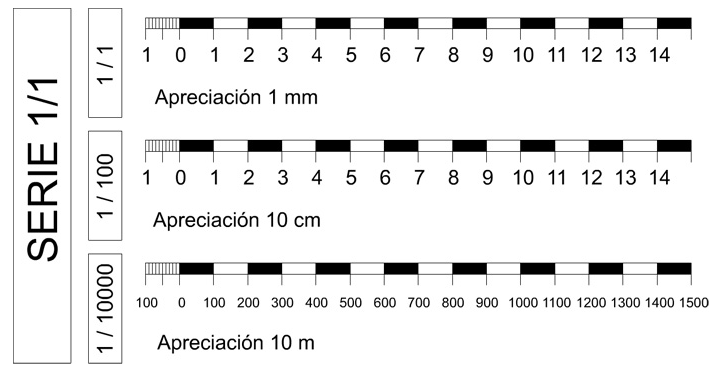
La escala en la que se trabaja se puede definir como una especie de regla o barra dividida en segmentos. Dichos espacios o segmentos representan las medidas reales representadas en kilómetros o metros y su respectiva equivalencia en centímetros o pulgadas.

Por ejemplo, en un plano de una casa un metro de construcción real, es representado por un centímetro en el plano. De esta manera cada trazo que se realice se puede pasar las medidas de manera rápida y fácil a la realidad.

¿Para qué sirven las Gráficas de Figuras con Escala?

La utilización de la grafica de figura con escala puede servir en la construcción de casa o edificios, ayudar en el modelado de monumentos o estructuras y facilitar el calculo de materiales. Pero también ayuda en conceptos más prácticos como los que veremos a continuación.

• Jerarquía visual: Para el diseño se de una nota de impacto también es importante representar los elementos más importantes según su tamaño relativo. De esta manera se crea una jerarquía según la importancia visual que tenga cada objeto.
• Adaptabilidad: Si las necesidades del modelo requirieran agrandar o reducir el diseño, la escala lo puede hacer y adaptarse sin ningún problema. Estos cambios pueden realizarse sin cambiar la exactitud de las medidas gracias a la escala y su implementación.
• Exactitud: Gracias a la exactitud que da la escala dentro de la figura gráfica, se pueden realizar mediciones distancias reales, sin necesidad de complicadas operaciones. Generalmente solamente se necesitaría una simple medición ya que se pueden transformar kilómetros o metros a solo centímetros o milímetros.

Tipos de Escalas

Se pueden dar tres tipos de escalas dentro de un diseño, las cuales se presentan de la siguiente manera:

• Reducción: La escala de reducción se da cuando la figura grafica es más pequeña que el modelo real. Se utiliza muy comúnmente en planos arquitectónicos o mapas. Ejemplo: 1:100, 1:50.
• Natural: Se refiere a aquella figura grafica que posee exactamente ala misma medida que el modelo de tamaño real. Ejemplo: 1:1.
• Ampliación: Se da cuando el dibujo es de mayor tamaño que el modelo de tamaño real. Es usado generalmente para representar piezas mecánicas que poseen un tamaño diminuto. Ejemplo: 10:1.

Pasos para Analizar la Graficas de Figuras con Escala

1. Medición de la gráfica: Con la utilización de una regla se debe hacer las medidas de la longitud de los lados del dibujo en centímetros.
2. Identificación de los Factores de Conversión.
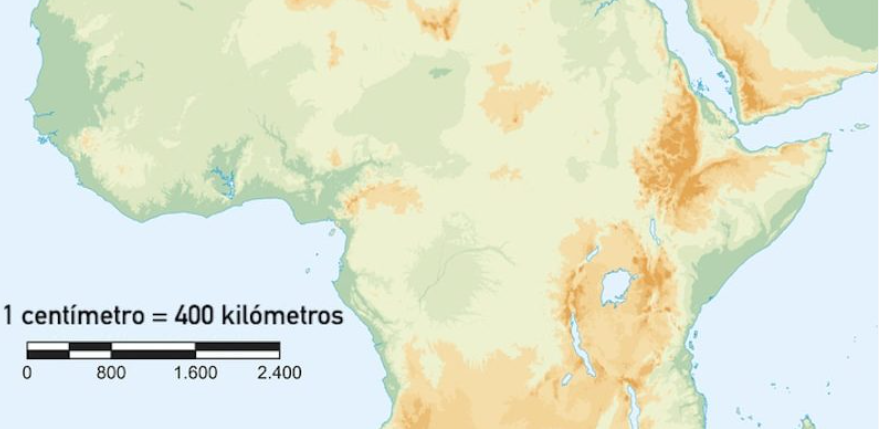
   1. Escala gráfica: Se compara la medida con la barra de la escala para confirmar cuantas unidades abarca de manera real.
   1. Escala numérica: Para obtener una medida real se multiplica la medida del dibujo (el digito que esta antes de los dos puntos) por el denominador (el digito después de los dos puntos). Ejemplo: 1:50, significa que cada centímetro (1 cm) equivale a 50 cm (1/2 metro) en el tamaño real.
3. Aplicación Formula básica: Para poder realizar una correcta interpretación de la escala se realiza la siguiente formula, Medida Real = Medida del Dibujo x Denominador de la Escala.

El análisis de graficas de figuras con escala son fundamentales para poder garantizar la comprensión y precisión de las medidas y proporciones entre el modelo grafica y el real. Gracias a esta exactitud en las medidas se pueden medir grandes distancias sin necesidad de hacer cálculos complicados.

Campos como la arquitectura, la geografía o la ingeniería y la mecánica suelen usar en gran manera este método para poder facilitar su trabajo.