Dentro de las Medidas de posición central podemos encontrar a la Moda, la cual es la medida que nos indica cual es el valor que más se repite. Esto quiere decir que su función es la de identificar el valor que posee una presencia con mayor frecuencia dentro del conjunto de datos.

La forma de identificarla, realmente es sencillo, solamente se debe de buscar el valor que aparece más veces. Sin embargo, en algunas bases de datos se puede carecer de una moda ya que sus valores solamente aparecen una solo vez.

También se puede dar el caso de datos Bimodales o Multimodales, los cuales se dan al presentarse dos o más valores que poseen la misma frecuencia máxima. En otras palabras, pueden existir valores que poseen la misma cantidad de apariciones, y que adicionalmente destaquen de los demás valores.

Forma de Identificación

Para que se pueda identificar la medida de la Moda de las demás medidas de posición central, es importante seguir los siguientes puntos:

• Identificar el valor más frecuente: Esto corresponde al valor que aparezca en mayor cantidad en comparación a los demás valores dentro del conjunto de datos. De una manera más simple es el valor que se repite más veces.
• Observación del conjunto de datos: Se debe prestar atención a todos los valores que se encuentren en las listas y categorías de la base de datos.
• Contar la frecuencia de cada valor: Para estar seguros de las apreciaciones anteriores, se debe determinar con exactitud cuantas veces aparece cada uno de los datos en el conjunto de información.

Características, Propiedades e Inconvenientes de la Moda

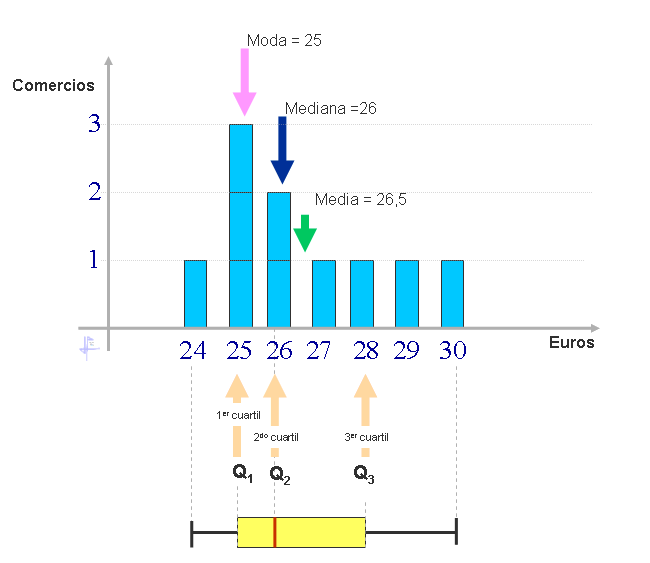
• Características:
  • Valor más común: Se define como el valor que más veces se repite.
  • Múltiples modas: Corresponde a un conjunto de datos que pueden poseer dos o más modas. Siempre y cuando dichos valores poseen la mayor cantidad de frecuencias y todos compartan la misma cantidad de repeticiones.
  • Sin moda: Si por otra parte los distintos valores solamente se repiten solamente una vez se establece que NO HAY MODA.
• Propiedades:
  • Representa un cálculo sencillo.
  • Posee una interpretación clara.
  • Como solamente depende de la frecuencia con la que se repite el valor, este se puede calcular como una variable cualitativa.
• Inconvenientes:
  • No siempre se puede situar en la parte central de la distribución.
  • Al poseer pocas observaciones dentro de grandes variaciones en los datos que se encuentran fuera de la moda, no afectaría de ninguna manera su valor.
  • Ya que su valor es independiente a la mayor parte de los datos indicados, lo hace sensible a las distintas variaciones de la muestra.
  • Se dan casos en la que existen más de una sola moda, ya que pueden existir dos o más valores con igualdad de frecuencia de apariciones.

Ejemplos de la Moda

• Ejemplo 1: Los alumnos de una clase indican su color favorito y dan la siguiente lista: azul, rosa, verde, azul, azul, amarillo, verde, azul, rosa, azul. Según esta información el color azul se repite 5 veces, el rosa 2 veces, el verde 2 veces y el amarillo solo 1 vez. En este caso el color azul es el que más se repite por lo que es la Moda.
• Ejemplo 2: Se cuenta la cantidad de personas que viajan en distintos vehículos en la carretera, dando como resultado: 7- 4-5- 6-9- 6-5- 1- 5-7-3- 6. Siendo que el número 5 y 6 son los que más se repiten en 3 ocasiones. De esta manera tenemos una medida bimodal.
• Ejemplo 3: En la asignatura de matemáticas, las calificaciones de los alumnos se dio de la siguiente manera: 80, 65, 70, 70, 92, 80, 96, 100, 70, 80, 92, 92. En esta circunstancia las notas de 70, 80 y 92 son las que se repiten más y con igual numero de veces “3”. Tomando estos valores en cuenta tenemos una medida multimodal.

Cuando los datos se encuentran agrupados en algún punto que divide el intervalo de moda en dos partes, en p y c-p. Siendo la “c” la amplitud del intervalo, la “n” la frecuencia absoluta perteneciente al intervalo de la moda y “ni-1” y “ni+1” como las frecuencias absolutas de un intervalo anterior y el posterior.

Importancia de la Medición Modal

La medición posicional de la Moda es de gran importancia dentro de los análisis estadísticos, ya que gracias a ella es posible identificar plenamente las tendencias en un conjunto de datos. Adicionalmente contribuye a la simplificación de la información, la toma de decisiones y la aplicación de los datos nominales.