En el campo de las medidas de posición y de manera oficial no se puede incluir al valor máximo como una medida oficial. Sin embargo, esta muy ligado a cada una de las medidas dentro del estudio de la estadística. Se puede definir como aquel valor que se encuentra en el punto más alto de un conjunto de datos o función.

De igual manera se puede indicar que el máximo se puede encontrar dentro de una función de cualquiera de las siguientes dos maneras:

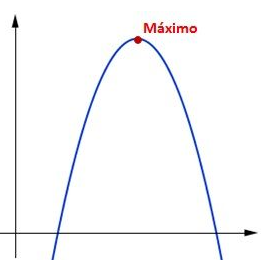
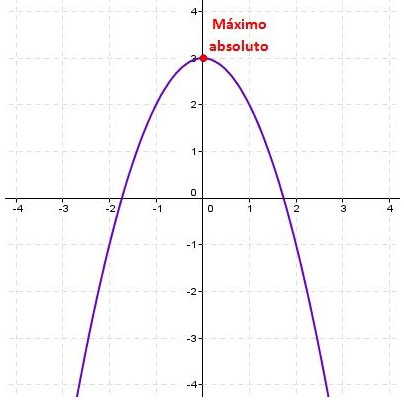
• Máximo Global: También conocido como “absoluto”. Ya que se refiere al valor más grande que se encuentra dentro de la función, tomando de esta manera todo su dominio.
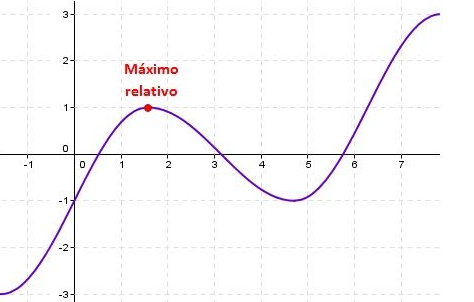
• Máximo Local: Se refiere a aquel valor que sea el más grande dentro de un intervalo especifico, dentro de una función. Pero esto NO significa que sea el más grande de toda la función.

Dentro de una función el máximo se encuentra ubicada en la coordinada “y”, en el punto más alto, ya sea global o local. Pero en dentro de un conjunto de datos representa al número más grande que se encuentre dentro de la base de datos.

Propiedades en una Función o Conjunto

El valor máximo posee sus propias propiedades que ayudan a localizarlo ya sea dentro de un conjunto de datos o en una función. A continuación, se podrá observar cada una de estas propiedades:

• Dentro de un Conjunto de Datos.
  • Unicidad: Según el principio de antisimétria, la cual proporciona una relación de orden en la base de datos, se indica que el máximo es un valor único.Cota Superior: Es considerado dentro de l conjunto como una cota superior (es el número igual o mayor que todos los demás números que se encuentren en el conjunto, función o sucesión).
  • Mayoría o igualdad: Dentro del conjunto es considerado como el valor que debe ser mayor o igual (al numero mayor) a los demás elementos existentes en el conjunto.
• Presente en una Función:
  • Global: Representa al mayor valor de todo el domino.
• • Relativo o Local: Es el punto más alto en un intervalo en “y”.
• • Valor Extremo: Según el Teorema de Valor Extremo, establece que, dentro de un conjunto cerrad. Debe alcanzar un máximo absoluto en su forma de Weierstrass.
• Calculo: Es posible encontrar su valor al calcular derivado de una función, si se iguala a cero al hallar los puntos críticos. De esta manera en la segunda derivada se confirmará si en efecto son los valores máximos locales, para luego hacer una comparación en los extremos del intervalo.

¿Cómo localizar el Máximo?

Nuevamente para encontrar este valor es importante seguir varias pautas. Dependiendo si se busca este dato dentro de una función o en un conjunto de datos.

• En una Función.
  • Derivada: Se da al calcular la primera derivada dentro de la función.Puntos Críticos: Al igualar la primera derivada a “cero”, se puede resolver la ecuación, en la cual se encontrarían los puntos críticos de la misma.Segunda Derivación: Al tener el valor de la primera derivación, se procede al calculo de la segunda derivada dentro de la función.Prueba: En los puntos críticos se debe evaluar los resultados de la segunda derivación
  .
  En caso de dar un resultado negativo, significaría que el máximo es local en ese punto.Extremos: Si se da un intervalo cerrado, se debe evaluar la función en los puntos finales del intervalo para intentar localizar máximos globales.
  • Comparación de valores: En los puntos críticos y en los extremos de los intervalos se debe comparar los valores de la función, para determinar los máximos globales.
• En un Conjunto de Datos.
  • Orden de los datos: Dentro de un conjunto de datos lo primero que se debe realizar es la organización de la información en una escala que va de menor a mayor.
  • Comparación: Al realizar una comparación según el orden de los valores, el que se encuentre de último en la lista será por ende el valor máximo.

Aplicaciones e Importancia del Máximo

Dentro de una función o en un conjunto de datos, el valor máximo es el más importante de localizar e identificar ya que para localizar. Ya que a partir de él se pueden obtener los problemas de optimización, verificar los costos y crear gráficos precisos con la información brindada.

De igual manera es un punto clave dentro de economía y la ingeniería ya que gracia a el se puede hacer un análisis de riegos eficiente. Así como la planificación estratégica y el mejoramiento de la eficiencia operativa.

Otras de las aplicaciones primordiales que se le pueda dar al Máximo es la del análisis de rendimiento, Riesgos financieros, ciencias ambientales, Diseño, modelado, planificación y ordenamiento de los procesos en diversos campos.