El inverso multiplicativo de un número es otro número que, cuando se multiplica por el primero, da como resultado el número uno. Dicho de otro modo, este mismo es el valor que, al combinarse en una multiplicación con el número original, produce uno. En los números reales el 0 no tiene inverso multiplicativo.

Si el número es una fracción, el inverso multiplicativo se obtiene invirtiendo el numerador y el denominador de esa fracción. Si el número es un entero, su inverso multiplicativo se representa como una fracción donde uno es el numerador y el número entero es el denominador.

La importancia del inverso multiplicativo

El concepto del inverso es fundamental en matemáticas, particularmente en el álgebra, permite simplificar expresiones, resolver ecuaciones y realizar divisiones con mayor facilidad. Para un número real a distinto de cero, el inverso multiplicativo es aquel número b que, al multiplicarse por a, da como resultado 1. Matemáticamente se expresa a x b= 1

El inverso multiplicativo es una herramienta que simplifica y facilita el manejo de operaciones matemáticas, siendo esencial para la resolución de ecuaciones y el manejo de fracciones y matrices, entre otros.

• Importancia en la resolución de ecuaciones:
  • El inverso multiplicativo es esencial en la resolución de ecuaciones, especialmente cuando necesitamos despejar una variable.
• En la división de fracciones:
  • Al dividir fracciones, el inverso multiplicativo permite transformar la operación en una multiplicación.
• En matrices y números complejos:
  • El concepto también se aplica en contextos avanzados, en el cálculo del inverso de una matriz o al trabajar con números complejos, donde facilita las operaciones y el análisis en estos sistemas.

¿Cómo sacar el inverso de un número?

El inverso de un número, también conocido como su recíproco, es aquel valor que, al multiplicarse por el número original, produce uno como resultado. Para obtener el inverso, basta con imaginar que intercambiamos la posición de la parte superior e inferior de una fracción. Si el número original no está expresado como fracción, simplemente lo convertimos, colocando el número uno en el lugar que corresponda. Esta relación se basa en la idea de que, al multiplicar el número por su inverso, el efecto de uno se “cancela” con el otro, dejando como resultado el uno.

Aquí tienes algunos ejemplos de cómo encontrar el inverso de distintos tipos de números:

• Número entero:
  • El inverso de 5 es 1/5
  • El inverso de -7 es -1/7
• Fracción:
  • El inverso de 2/3 es 3/2
  • El inverso de -4/5 -5/4
• Número decimal:
  • El inverso de 0.5 es 2 (porque 0.5 es equivalente a 1/2
  • El inverso de 0.25 es 4 (ya que 0.25 equivale a 1/4
• Número mixto:
  • El inverso de 1 y 1/2 es 2/3 (primero convierte el número mixto en fracción impropia: 3/2 luego invierte para obtener 2/3
• Estos ejemplos muestran cómo podemos aplicar el concepto del inverso en diferentes tipos de números para simplificar operaciones.

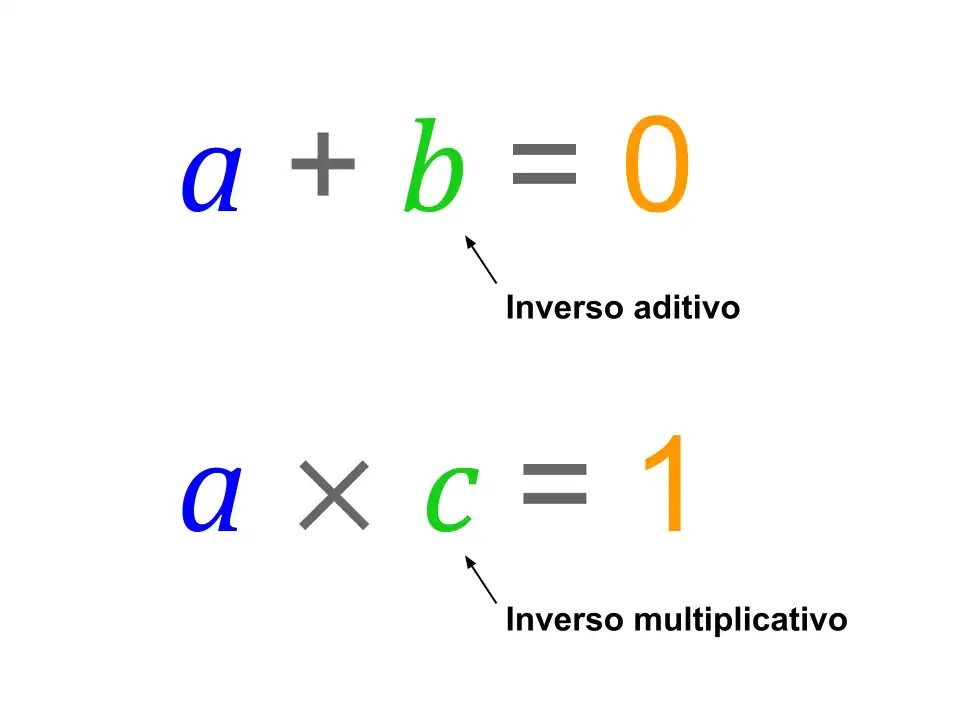
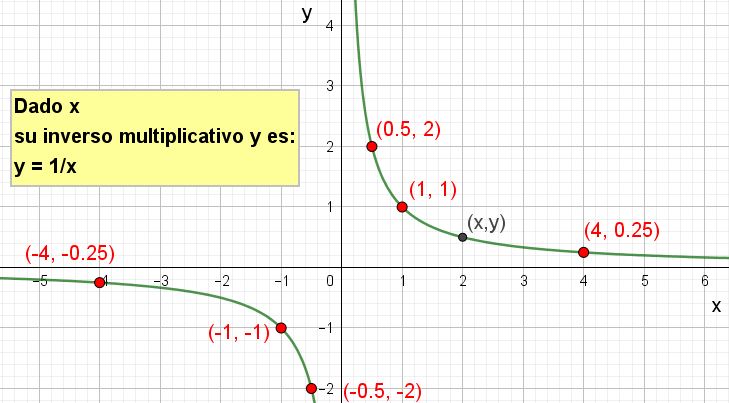
Inverso multiplicativo en la recta numérica

En una recta numérica, el inverso de un número está ubicado a una distancia proporcional inversa al valor original desde el punto de origen (cero). Esta representación ayuda a visualizar que, cuanto más grande es un número, su inverso multiplicativo es proporcionalmente más pequeño, acercándose a cero y viceversa.

Te explico cómo ubicarlo según el tipo de número:

• Número entero mayor que uno:
  • Si tienes un número entero positivo, su inverso multiplicativo será una fracción que se encuentra entre cero y uno en la recta numérica.
  • El inverso multiplicativo de 4 (ubicado a la derecha de cero) es un cuarto, que se encuentra más cerca de cero en la misma dirección positiva.
• Fracción propia (valor entre cero y uno):
  • Si tienes una fracción como un medio (o 0.5), su inverso multiplicativo será un número mayor a uno (en este caso, 2), que estará más lejos de cero en el mismo lado de la recta.
  • En el caso de un tercio, su inverso multiplicativo será 3.
• Número negativo:
  • Para un número negativo, el inverso multiplicativo será también negativo y se ubicará en el lado izquierdo de la recta.
  • Por ejemplo, el inverso de -2 es -un medio, que estará más cerca de cero en el lado negativo de la recta.
• Número uno y menos uno:
  • El número uno es especial, ya que su inverso multiplicativo es también uno. Lo mismo ocurre con menos uno; su inverso multiplicativo es igualmente menos uno.
• Ejemplo gráfico en la recta numérica:
  • Si imaginamos la recta numérica, se vería algo así:
    • Para el número 2, su inverso multiplicativo (un medio) estaría en el mismo lado de cero pero más cerca de él.
      • Para “un tercio”, el número 3 estaría más lejos de cero en el mismo lado positivo.

Propiedades clave del inverso en matemáticas

El concepto de inverso en matemáticas se refiere a una entidad que, al combinarse con otra mediante una operación específica, produce un resultado neutro. Esto puede entenderse en dos sentidos principales: el aditivo y el multiplicativo. En el caso del inverso aditivo, el objetivo es encontrar un número que al sumarse con otro, dé como resultado cero, neutralizando así el valor inicial.

Para el inverso, el propósito es hallar un valor que, al multiplicarse con otro, produzca uno, lo cual anula el efecto de la multiplicación original. Estas propiedades son fundamentales porque permiten deshacer operaciones y resolver ecuaciones en matemática.

Comprender este concepto es fundamental, porque facilita la realización de operaciones como la división de fracciones y la resolución de ecuaciones en las que necesitamos “deshacer” multiplicaciones. Aprender a identificar y utilizar el inverso multiplicativo permite una mayor flexibilidad y comprensión en el manejo de fracciones y otros números racionales. Este conocimiento no solo simplifica problemas matemáticos cotidianos, sino que también sienta las bases para un aprendizaje más profundo en álgebra y matemáticas avanzadas.