Una célula es la unidad básica de la vida y la estructura fundamental de los organismos vivos. Todos los seres vivos están compuestos por células. Ya sean unicelulares (como bacterias y protozoos) o multicelulares (como plantas, animales y hongos), que están formadas por muchas células.
La célula es la entidad más pequeña de los seres vivos
La célula es considerada la unidad más pequeña de los seres vivos y es la estructura básica de la vida. Todos los organismos vivos, ya sean unicelulares o multicelulares, están formados por células. Las células son la unidad fundamental de la organización biológica. Que llevan a cabo las funciones esenciales para la supervivencia y el desarrollo de los organismos. La teoría celular establece que todos los seres vivos están compuestos por células y que la célula es la unidad básica de la vida.
La sinfonía microscópica de la vida
En el tejido invisible que sustenta la existencia las células. Dan inicio a una sinfonía microscópica una obra maestra de complejidad y armonía que orquesta la maravilla de la vida. Bajo el lente del microscopio, exploramos este mundo diminuto. Donde cada célula desempeña su papel, contribuyendo a la melodía incesante de la supervivencia y el crecimiento.
Desde el núcleo, donde se resguarda la partitura genética que guía cada movimiento. Hasta los intrincados pasillos del retículo endoplasmático. Donde las notas de proteínas danzan y se ensamblan, cada organelo contribuye a la composición única de cada célula. Las mitocondrias, como músicos energéticos, ejecutan una danza constante para proporcionar la vitalidad que impulsa la actuación.
A través del citoesqueleto, las células mantienen su estructura y coordinan los movimientos, como si fueran bailarinas en un escenario invisible. El delicado equilibrio de esta sinfonía microscópica se revela en el aparato de Golgi. Donde se empaquetan y distribuyen las notas esenciales para el funcionamiento celula
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en líneaTipos de células
Las células son las unidades fundamentales de la vida. Se dividen en dos categorías principales: procariotas y eucariotas, según la presencia o ausencia de una membrana nuclear. Que rodea al núcleo. Las células procariotas, representadas por bacterias y arqueas. Exhiben una estructura más simple, con el material genético dispuesto en un nucleoide sin membrana y la carencia de organelos rodeados por membranas.
¿Qué son las Células procariotas?
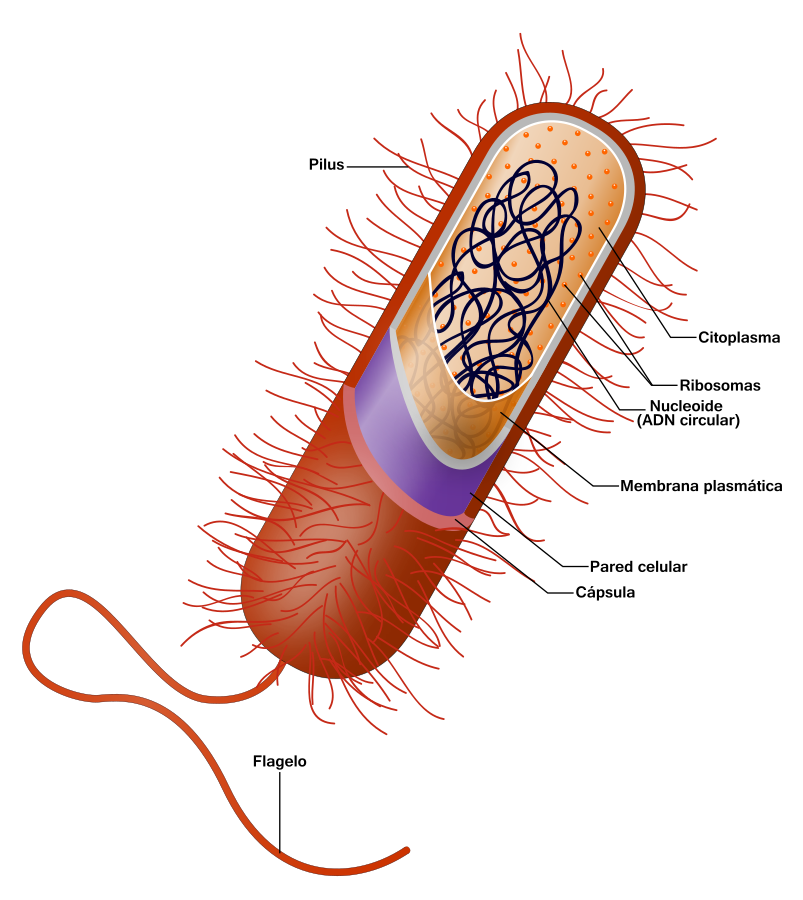
Las células procariotas son un tipo de células que se caracterizan por no tener un núcleo definido rodeado por una membrana. En lugar de un núcleo, el material genético, generalmente ADN circular. Se encuentra en una región central llamada nucleoide, que carece de una membrana que lo separe del resto de la célula. Estas células son más simples en estructura que las células eucariotas y carecen de organelos membranosos especializados.
Algunas características clave de las Células procariotas incluyen:
- Núcleo sin membrana: Como se mencionó, no tienen un núcleo definido con membrana que aísle el material genético.
- Tamaño más pequeño: En general, las células procariotas son más pequeñas que las células eucariotas.
- Organelos limitados: Carecen de organelos membranosos como mitocondrias, retículo endoplasmático y complejo de Golgi.
- Pared celular: Muchas células procariotas tienen una pared celular que proporciona resistencia y forma a la célula.
- Flagelos: Algunas células procariotas tienen flagelos que les permiten moverse.
¿Qué son las Células eucariotas?
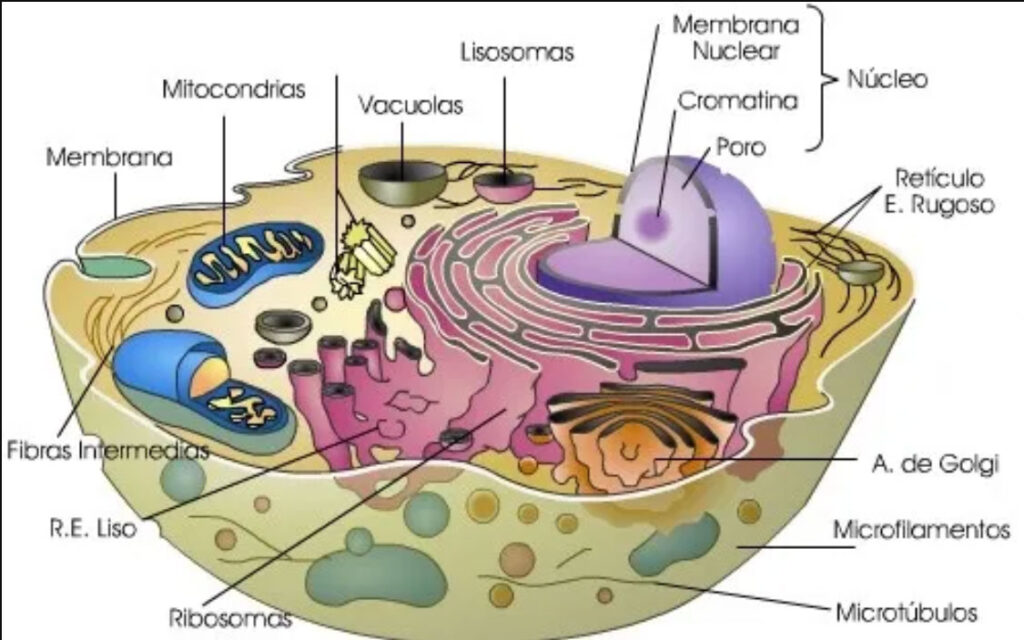
Las células eucariotas son un tipo de célula que se caracteriza por tener un núcleo definido y delimitado por una membrana nuclear. Estas células también poseen organelos membranosos, como mitocondrias, retículo endoplasmático y complejo de Golgi, que realizan diversas funciones especializadas dentro de la célula.
Algunas características clave de las células eucariotas incluyen:
- Núcleo definido: El material genético de las células eucariotas está contenido en un núcleo separado del resto de la célula por una membrana nuclear. Este núcleo alberga el ADN de la célula.
- Organelos membranosos: Además del núcleo, las células eucariotas contienen organelos membranosos especializados. Como las mitocondrias (encargadas de la producción de energía). El retículo endoplasmático (que participa en la síntesis de proteínas y lípidos), y el complejo de Golgi (que modifica y empaca proteínas para su transporte).
- Tamaño variable: Las células eucariotas pueden ser de diversos tamaños y formas. Constituyen la base de la mayoría de los organismos multicelulares, como plantas, animales, hongos y protistas.
- División celular compleja: Las células eucariotas se reproducen a través de un proceso llamado mitosis. Que implica la división del núcleo y la posterior división celular para generar células hijas genéticamente idénticas.
¿Qué son las Células animales?
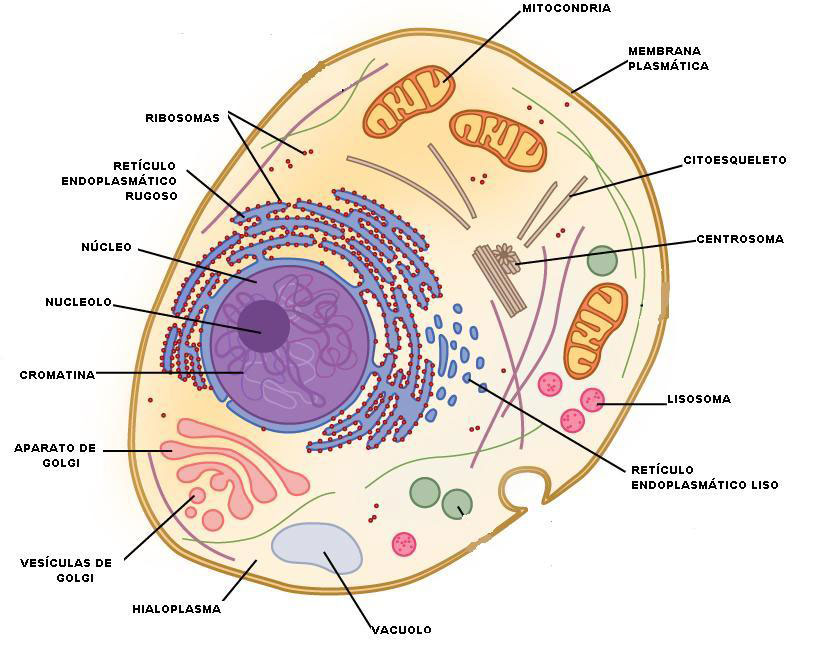
La célula animal es un tipo de célula eucariota que constituye los componentes básicos de los tejidos y órganos de los animales. Estas células comparten muchas características con otras células eucariotas, pero también tienen algunas particularidades que las distinguen, especialmente en comparación con las células vegetales.
Algunas características clave de las células eucariotas incluyen:
- Núcleo definido: Al igual que todas las células eucariotas, las células animales tienen un núcleo definido que contiene el material genético de la célula. Esta protegido por una membrana nuclear.
- Organelos membranosos: Las células animales contienen varios organelos membranosos. Como mitocondrias responsables de la producción de energía y el retículo endoplasmático que participa en la síntesis de proteínas y lípidos). Un complejo de Golgi (modifica y empaca proteínas). y lisosomas (vesículas que contienen enzimas digestivas).
- Citoesqueleto: Las células animales tienen un citoesqueleto, una red de filamentos proteicos que proporciona soporte estructural, mantiene la forma celular y facilita la movilidad.
- Membrana celular: La membrana celular rodea la célula animal, controlando el paso de sustancias dentro y fuera de la célula y proporcionando una barrera selectiva.
- Centríolos: Muchas células animales contienen centríolos, estructuras cilíndricas que desempeñan un papel en la división celular.
- No poseen pared celular: A diferencia de las células vegetales, las células animales no tienen una pared celular rígida. En su lugar, están rodeadas por una membrana celular flexible.
¿Qué son las Células vegetales?
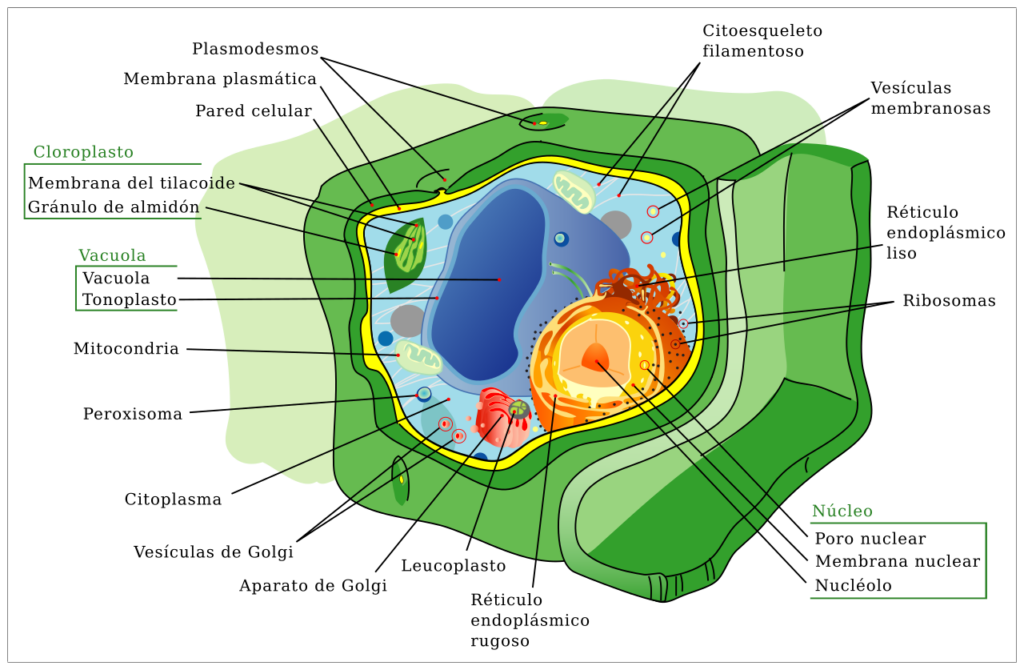
Las células vegetales son un tipo de célula eucariota que forma parte de los tejidos y órganos de las plantas. Aunque comparten muchas características con las células animales y otras células eucariotas. Las células vegetales también tienen características distintivas que las adaptan a las funciones específicas de las plantas.
Algunas características clave de las Células vegetales incluyen:
- Pared celular: Una característica distintiva de las células vegetales es la presencia de una pared celular rígida compuesta principalmente de celulosa. La pared celular proporciona soporte estructural a la célula y a la planta en su conjunto.
- Núcleo definido: Al igual que otras células eucariotas, las células vegetales tienen un núcleo definido que alberga el material genético de la célula. Que esta protegido por una membrana nuclear.
- Organelos membranosos: Las células vegetales contienen varios organelos membranosos incluyendo mitocondrias. Encargadas de la producción de energía, retículo endoplasmático (participa en la síntesis de proteínas y lípidos). Con un complejo de Golgi (modifica y empaca proteínas) y cloroplastos (realizan la fotosíntesis).
- Cloroplastos: La presencia de cloroplastos es una característica única de las células vegetales. Estos organelos contienen clorofila y son responsables de realizar la fotosíntesis, convirtiendo la luz solar en energía química.
- Vacuola central: Las células vegetales suelen tener una gran vacuola central, una vesícula membranosa llena de líquido. Que desempeña un papel en el mantenimiento de la turgencia celular y el almacenamiento de sustancias.
- Citoesqueleto: Al igual que las células animales, las células vegetales tienen un citoesqueleto que proporciona soporte estructural y facilita el transporte intracelular.
- No tienen centríolos: A diferencia de las células animales, las células vegetales generalmente no contienen centríolos.
Partes fudamentales de la célula
- Membrana plasmática o citoplasmática: presente en células eucariotas y procariotas. Es una membrana que divide la parte exterior de la parte interior de la célula. Está formada por una doble capa continua de fosfolípidos, proteínas intercaladas o adheridas a su superficie. Las funciones de esta membrana son dar forma y estabilidad a la célula, separar el contenido interno de la célula del medio que la rodea.
- Pared celular: presente en células procariotas y en células eucariotas de plantas, hongos y algas. Es una capa gruesa y bastante rígida que está localizada en la parte externa de la membrana plasmática. Le confiere resistencia y estabilidad a la célula. Su composición varía según el tipo de célula.
- Núcleo: presente en células eucariotas. Contiene casi todo el material genético (ADN) de la célula y está rodeado por una envoltura nuclear que contiene poros. Sus principales funciones son almacenar la información genética, controlar las actividades de todos los orgánulos y coordinar la reproducción celular.
- Nucleoide: presente en células procariotas. Es una región en la que se encuentra el ADN, que en las células procariotas es una única molécula con forma circular y cerrada. A diferencia del núcleo en células eucariotas, el nucleoide no tiene envoltura nuclear.
- Citoplasma: presente en células eucariotas y procariotas. Es la parte de la célula que se ubica entre la membrana citoplasmática y el núcleo. Está constituido por una parte líquida llamada “citosol”, que se compone de agua, iones y proteínas. En el citosol están sumergidos todos los orgánulos.
¿Qué funciones cumplen las células?
Las células desempeñan un papel crucial en la vida de los organismos. Ya que realizan una variedad de funciones esenciales para su supervivencia y funcionamiento adecuado. En primer lugar, proporcionan la estructura fundamental para la construcción de tejidos y órganos, ofreciendo soporte físico a la arquitectura biológica del organismo. Además, las células almacenan y transmiten la información genética a través del ADN. Asegurando la continuidad de la herencia y la transmisión de rasgos a las generaciones futuras.
Algunas de sus funciones fundamentales son:
- Estructurales: las células pueden formar tejidos, como el tejido adiposo (grasa), el tejido muscular y el tejido óseo (huesos). Que dan soporte al cuerpo de los animales y a sus órganos.
- Secretoras: las células pueden sintetizar sustancias que luego secretan al medio extracelular. Ya que sea porque estas sustancias realizan funciones en el exterior de la célula o porque son sustancias de desecho.
- Metabólicas: las células llevan a cabo reacciones químicas necesarias para obtener energía y las sustancias necesarias para realizar sus distintas funciones. En este sentido, pueden sintetizar compuestos químicos o descomponerlos.
- Defensivas: Algunas células contribuyen a eliminar patógenos y combatir enfermedades. Este el caso de los linfocitos T son células que reconocen de manera específica ciertos antígenos, que luego destruyen. También destruyen células propias del cuerpo que fueron infectadas con enfermedades.
- Interacción o relación: Las células reaccionan a estímulos tanto internos como externos, y generan una respuesta
- Reproductoras: las células eucariotas se pueden dividir por mitosis (células somáticas) y por meiosis (células germinales). Mientras que las células procariotas se pueden dividir por fisión binaria. Por ejemplo: los espermatozoides son células que se originan de células germinales cuando se dividen por meiosis.
Teoría celular de biologia moderna
La teoría celular es un principio fundamental en biología que establece que todos los organismos vivos. Que están compuestos por células. Ya que la célula es la unidad básica de la vida, y que todas las funciones vitales de un organismo ocurren dentro de las células. La teoría celular ha evolucionado a lo largo del tiempo, pero sus principios fundamentales siguen siendo la base de la biología moderna.
Esta teoría es esencial para entender la biología y ha sido crucial. Para el avance de la investigación en medicina, genética, microbiología y otras disciplinas relacionadas con la biología. Desde su formulación en el siglo XIX por científicos. Como Matthias Schleiden, Theodor Schwann y Rudolf Virchow y lo largo de los años ha evolucionado con nuevos descubrimientos y tecnologías.
En resumen, la célula es la piedra angular de la vida, una estructura intrincada y sorprendente. Que continúa fascinando a los científicos y desbloqueando secretos fundamentales de la existencia. La investigación continua en este campo promete revelar aún más sobre la naturaleza esencial de la vida. Cómo podemos aplicar ese conocimiento para mejorar la salud. Sin duda la tecnología y nuestro entendimiento del mundo que nos rodea y en general entender las estructura de nuestro cuerpo.









