Se puede definir al número como un objeto matemático que se utiliza para contar distintas cantidades, medir diferentes magnitudes o etiquetar objetos para su organización. Sin embargo, existen distintas representaciones de los números.
Esto quiere decir que existen muchas formas diferentes para poder representar un mismo número o el mismo valor. Ya sea por medio de palabras, cifras arábigas, fracciones, decimales, porcentajes, números romanos o descomposición posicional.
El concepto número en el término común en el que lo utilizamos se refiere puntualmente a las cifras arábigas. Las cuales corresponden a la numeración decimal que usamos para representar cualquier número o cantidad. Su nombre proviene de los comerciantes árabes que los difundieron por Europa, aunque su origen real proviene de la India.
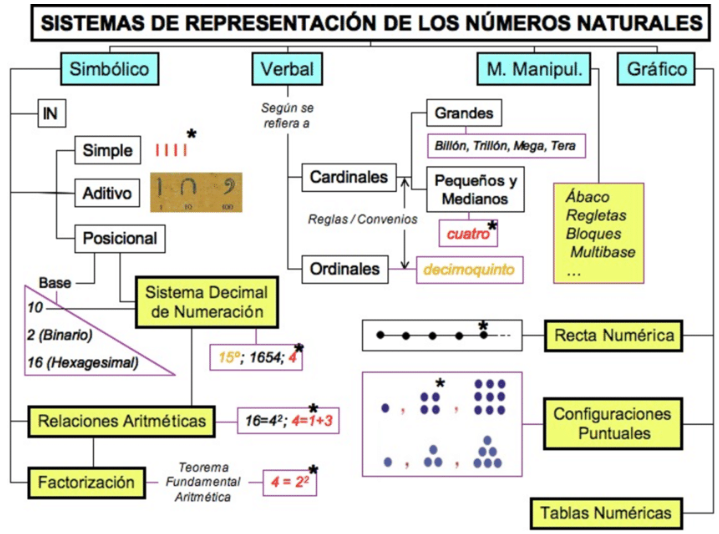
Diferentes tipos de Números
De esta manera una misma cantidad puede ser representada de muchas maneras diferentes. Pero también se puede encontrar diferentes formas de representaciones de los números. Como los números naturales, enteros, racionales, Irracionales y los complejos.
- Naturales: Que se representa con el siguiente símbolo N y son aquellos números que incluyen los primos y compuestos, así como los positivos (1, 2, 3, 4, 5, 6 7, 8, 9, 0) y negativos.
- Enteros: Utiliza el símbolo de la Z e incluyen a los números naturales y también las fracciones.
- Racionales: Utiliza el símbolo de la Q e incluye a los números naturales y enteros.
- Irracionales: Se identifican con la letra I y en ellos se incluyen los números que se representan de otras maneras como la raíces (√) o el valor de pi (𝜋).
- Reales: Usa el símbolo de R e incluye los números racionales e Irracionales.
- Complejos: Usan el símbolo de C e incluyen todos los números reales más los imaginarios.
Ejemplos de Distintas Representaciones de los Números
Para poder tener una mejor referencia sobre las distintas representaciones de los números a continuación se brinda un ejemplo de cada una de ellas.
- Cifras numéricas: Generalmente es la manera más común de representar a los números.
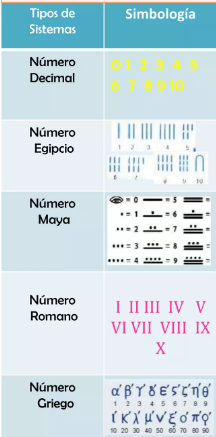
- Romana: Se refiere al sistema numérico Romano que usa siete letras del abecedario para conformar distintas cantidades gracias a sus diferentes combinaciones. Estas son 1 (l), 5 (V), 10 (X), 50 (L), 100 (C) y 1000 (M). Ejemplo: MCML.
- Arábiga: Se refiere al sistema decimal que usamos comúnmente, 1, 2, 3, 4, 5, 6, 7, 8, 9 y 0. Ejemplo 1350.
- Palabras: Esta representación en por medio de palabras, aunque varia dependiendo del idioma en el que se presente.
- Español: Mil trecientos cincuenta (1350).
- Ingles: One thousand three hundred fifty (1350).
- Frances: Mille trois cent cinquante (1350).
- Fracciones: Es cuando se representa una cantidad en relación a dos números enteros.
- 1/2
- 3/6
- Descomposición Posicional: Indica el valor de cada digito, de acuerdo a su posición.
- 1350: 1 x1000 + 3 x 100 + 5 x 10 + 0 x 1.
- Porcentajes: Son aquellas representaciones de una porción de una totalidad, por lo general representada como el 100%.
- La mitad de 100% es de 50% o de ½ (fracción).
- Decimales: Se refiere a aquellas cantidades que poseen un separador (coma) que indica la notación decimal.
- 0.5.
Importancia de las Distintas Representaciones de los Números
En diferentes ocasiones debemos representar una misma cantidad, número o digito de maneras diferentes para obtener representaciones diversas. Esto se puede usar en campos como el legal o político en donde por lo general se usa la representación de los palabra o arábiga.
Adicionalmente en campos matemáticos como la estadística, finanzas o de investigación se puede usar la fracción, la arábiga, el porcentaje o decimales. Todo depende del contexto en el que se use o en tipo de problema que se quiere representar su solución o información.
La importancia de las distintas representaciones de los números se basa primordialmente de la flexibilidad para expresar una cantidad. Los números aportan múltiples formas para resolver problemas, organizar objetos, realizar cuentas, visualizar operaciones (suma, resta, multiplicación y división), entre muchas otras cosas.
Sus distintas representaciones pueden facilitar su visualización o la comunicación de ideas o resultados, permitiendo la conexión entre distintos lenguajes matemáticos. Tomando esto en cuenta cada representación facilita el entendimiento en el mundo de las matemáticas.
