Cuando se habla sobre las frecuencias porcentuales nos referimos a aquellas que dan el porcentaje de cada observación dada según la categoría o el valor. Todo esto dentro de un conjunto de datos que se obtiene al multiplicar la frecuencia relativa por 100.
Se debe recordar que la suma total de las frecuencias siempre debe de ser 100%, lo que nos indica que se abarco la totalidad de la muestra analizada. Las frecuencias suelen dividirse en dos tipos principales que son la absoluta y la relativa, pero a su vez de estas se puede identificar a la absoluta acumulada y a la relativa acumulada.
Tipos de Frecuencias Porcentuales
Dentro del campo de la estadística se puede ubicar cuatro tipos de frecuencias, las cuales son las más comunes de utilizar.
- Absoluta: La frecuencia absoluta se define como el número de veces que un valor se repite como resultado, dentro de un conjunto de datos.
- Relativa: Cuando se refieren a la frecuencia relativa es aquella porción de cada frecuencia absoluta existente. En otras palabras, es la el resultado de dividir a la frecuencia absoluta entre el total de datos de la muestra.
- Formula: Si partimos desde el hecho que para obtener como resultado el conjunto total de datos o frecuencia relativa(fi). Se debe dividir la frecuencia absoluta (ni) entre el tamaño de la muestra (N).
- Por otro lado, si tomamos a la frecuencia relativa y la multiplicamos por 100 nos indicara la frecuencia porcentual existente.
- Absoluta acumulada: Al total de las frecuencias absolutasde las muestras menores o iguales de un cierto valor dentro de una lista ordenada, se le denomina frecuencia absoluta acumulada.
- Relativa acumulada: Para obtener el valor de la frecuencia relativa acumulada de debe dividir a la frecuencia absoluta acumulada entre en total de la muestra analizada.
Ejemplos de Frecuencias
Ejemplo #1: Si en un grupo que se compone por 20 estudiantes, se desea conocer el porcentaje de los que pudieron aprobar el examen. Y se brinda como datos que 5 de los 20 estudiantes reprobaron la prueba.
- Datos: aprobados 15 y reprobados 5.
- Frecuencia Absoluta: Total de aprobados 15 y total de reprobados 5.
- Frecuencia Relativa: Aprobados (15/20= 0,75) y Reprobados (5/20= 0,25).
- Frecuencias porcentuales: Aprobados (0,75*100= 75%), Reprobados (0.25*100= 25%)
En respuesta se puede indicar que el 25% de los estudiantes reprobaron el examen, mientras que el 75% si lo aprobó.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
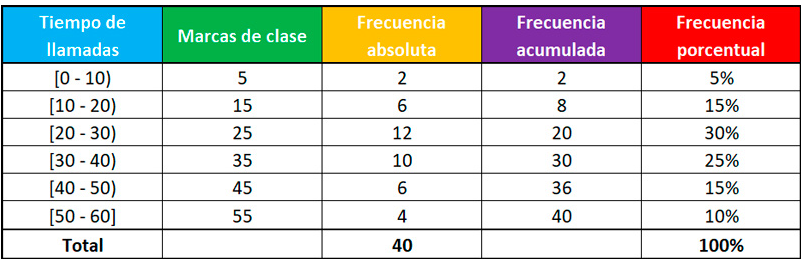
en líneaEjemplo #2: En un aula se analizan las calificaciones de los estudiantes, las cuales fueron las siguientes: 18, 13, 12, 14, 11, 08, 12, 05, 15, 20, 18, 14, 15, 11, 10, 11, 11, 10. Tomando los datos anteriores se analiza lo siguiente.
- Frecuencia absoluta: El número 11 se repite en 4 ocasiones.
- Frecuencia relativa: Se divide la mayor cantidad de veces aparecidas (4) entre el total de notas (18). 4/18= 0,22, eso quiere decir que la frecuencia relativa de 11 es 0,22.
- Frecuencia absoluta acumulativa: De 11 el valor absoluto acumulativo es 8, ya que hay 8 notas iguales o menores a 11.
- Frecuencia relativa acumulativa: Se divide la frecuencia absoluta acumulativa (8) entre el total de notas (18). Resultando que 8/18= 0.44, por lo que la relativa acumulativa de 11 es 0,44.
- Frecuencias Porcentuales: Se multiplica la frecuencia relativa (0,22) por 100. Esto da como resultado que 0,22*100= 22%.
El resultado indica que el 22% de los estudiantes obtuvieron una nota de 11 en el examen.
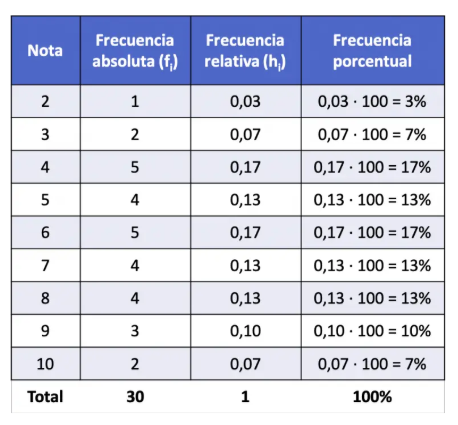
Importancia de las Frecuencias Porcentuales
Para varios campos en los cuales se pueden aplicar las frecuencias porcentuales. Es de gran importancia entender como su uso dentro de los análisis ayuda a la simplificación de la información. Pero adicional a esto se pueden dar otros puntos importantes primordiales.
- Comparación: Estas frecuencias permiten facilitar la comparación entre los porcentajes en diferentes conjuntos de datos.
- Análisis de datos: Permite de una manera clara y simple la distribución de una muestra o población entre diferentes categorías.
- Comunicación: son una forma efectiva y simple de hacer llegar la información de los resultados, ya sea por medio de gráficos o tablas a más personas.
- Resumir datos: Permite que grandes conjuntos de información se puedan resumir de una manera concisa y clara. Permitiendo también hacer enfoques únicamente en las categorías o puntos de interés.
- Visualización de datos: Permite sintetizar toda la información en tablas o diferentes tipos de graficas. De manera que se pueda ver y comparar toda la información en una sola imagen.
En síntesis, las frecuencias potenciadoras, ayuda a condensar la información más relevante dentro de los conjuntos de datos. Para después mostrarlos de una manera fácil, concisa, clara y simple toda la información importante en imagines, tablas o graficas fáciles de analizar. Esta herramienta ahorra tiempo a la hora de dar a conocer los datos, permitiendo dar paso al análisis en lugar de perderlo al tener que analizar todo el conjunto completo.









