Las medidas de variabilidad también son conocidas también en el campo de las matemáticas como las medidas de dispersión (propagación). Se define como aquellas medidas que cuantifican que tan dispersos se encuentran los diferentes datos dentro de un conjunto en relación a un valor central.
Dentro de estas medidas podemos obtener las medidas de rango, varianza, rango intercuartílico, desviación y coeficiente de variación. Todas estas medidas o métricas son de gran importancia para poder determinar si un valor central es un buen representante del conjunto estudiado.
Las llamadas propiedades de las distribuciones, suelen conformarse por las medidas de variabilidad que se contrastan directamente con la tendencia central o la ubicación. En la mayoría de estas medidas de dispersión se da que las cantidades que se miden poseen las mismas unidades de medida.

La Medidas de Dispersión más Comunes
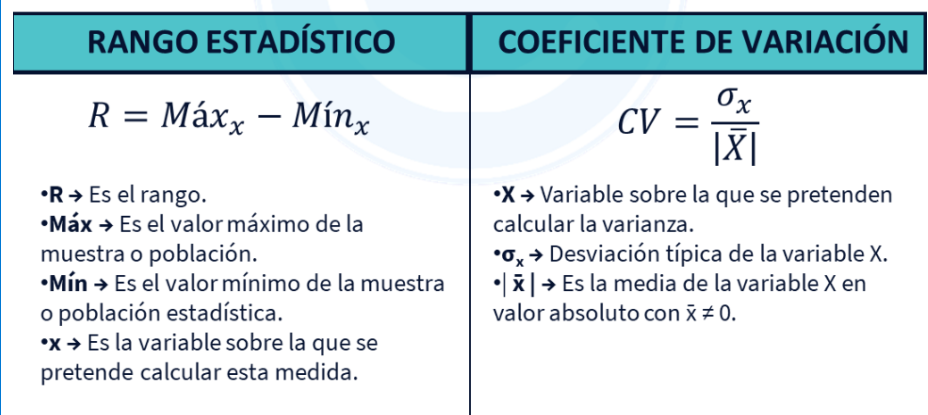
- Rango: Se refiere a la diferencia que existe los valores máximos y mínimo de un conjunto de datos. Aunque se trata de una medida muy simple, se puede ver afectada por algunos valores atípicos.
- Rango Intercuartílico: También se le puede asignar el signo de (RIC) y se calcula con la diferencia del tercer cuartil (Q3) y el primer cuartil (Q1). Por tanto, esta medida representa a la dispersión del 50% central de los datos, esto hace que sea menos sensible de los valores extremos por el rango.
- Varianza: Se encarga de medir la dispersión promedio que se encuentra en los datos que calculan el promedio de la diferencia al cuadrado. Esto en cada punto con respecto a la medida usada.
- Desviación Estándar: Es la raíz cuadrada encontrada en la varianza. Brinda una medida de la distancia en promedio de los datos que se pueden encontrar respecto a la medida. Posee una fácil interpretación ya que se expresa en las mismas unidades que los datos originales.
- Coeficiente de Variación: Puede expresar la desviación de forma estándar en relación con la media. Permite comparar la variabilidad de los conjuntos de datos con distintas magnitudes y unidades.
Importancia de las Medidas de Variabilidad
Al estudiar más sobre las medidas de variabilidad, queda claro que posee varios puntos importantes.
- Dispersión: Permite entender si los datos son más consistentes, agrupados o si por el contrario están ampliamente dispersos.
- Tendencia Central: Determina que tan representativa es la mediana o media que se encuentran en el conjunto de datos. Si un promedio presenta alta variabilidad puede que este no se un buen resumen de datos.
- Comparación de los Conjuntos de Datos: Compara la dispersión que existe entre los grupos cuando se usan variables con distintas unidades de medida. Al igual que como pasa con el coeficiente de variación.
Otras Medidas de Variabilidad
Además de las medidas más comunes, existen otras que pertenecen a las medidas de variabilidad, pero no son tan conocidas o utilizadas. Se les conocen como adimensionales ya que no tienen unidades, inclusive si la variable en sí posee unidad. Algunas de ellas son:
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea- Coeficiente de variación.
- Deferencia media relativa.
- Coeficiente de dispersión cuartil.
- Entropía.
- Varianza.
- Relación de Varianza a media.
Estas otras medidas son menos comunes de medir por un solo número. Algunas de ellas poseen fines especializados entre ellos las varianzas como la de Hadamard y la de Allan.
Fuentes de las Medidas de Dispersión
- Ciencias Físicas: En estos casos la variabilidad se puede dar gracias a resultados erróneos de algunas mediciones aleatorias. Sin embargo, las mediciones hechas a base de instrumentos suelen ser muy precisas. En este caso el error se daría en el momento en que el evaluador analiza dichos resultados.
- Ciencias Biológicas: En esta rama la muestra que se mide, muy rara vez es estable o inmutable. La variabilidad que se observa suele ser intrínseca dependiendo del fenómeno. En otras palabras, se presenta una variabilidad intraindividual, esto quiere decir que miembros distintos de una misma población pueden diferir en los resultados.
- Finanzas y Economía: Tanto en estas como en otras ramas, se puede presentar el análisis de regresión el cual intenta explicar como la dispersión dentro de una variable independiente es medida generalmente por su varianza.
Orden Parcial de las Medidas de Variabilidad
El ordenamiento parcial de una medida de dispersión se da dentro de una distribución de preservación y de la distribución de probabilidad, tomando en cuenta su dispersión. En estas dos distribuciones se da cuando una puede calificarse como que posee una mayor dispersión que la otra.
Como estos valores pueden variar no se puede asegurar con certeza que una tenga más dispersión que todas las demás. Por otra parte, presenta las siguientes características:
- El rango se cataloga como una medida que se cataloga con la amplitud del conjunto de datos.
- Es sensible a los diferentes valores externos.
- No se da razón de la variabilidad de los datos de un valor particular o de una medida de tendencia central.
- Se da en las mismas medidas que la variable de estudio.
Las medidas de variabilidad identifican el tipo de dispersión presente en los conjuntos de datos, indicando que tan parecidos o diferentes son de los valores que se observan. Son indispensables en la medida de la tendencia central, aunque en ocasiones podrían ser engañosas.









