Cuando se desea expresar cantidades muy pequeñas, se utilizan los submúltiplos. Los cuales utilizan la potencia de 10 para expresar las cantidades de manera más sencilla y corta. Según el Sistema Internacional de Medidas (SI) se establece una unidad base para cada medida por ejemplo el metro cubico para el volumen, el gramo para la masa o el metro para la distancia.
En términos sencillos para evitar dar cantidades muy largas. Con muchos dígitos se utilizan los múltiplos para las cantidades mayores a la unidad base y para las cantidades menores se usa los submúltiplos. Siguiendo la metáfora de la escalera, los tres submúltiplos más cercanos a la unidad base son los que se utilizan con mayor frecuencia, aunque existen mucho más.
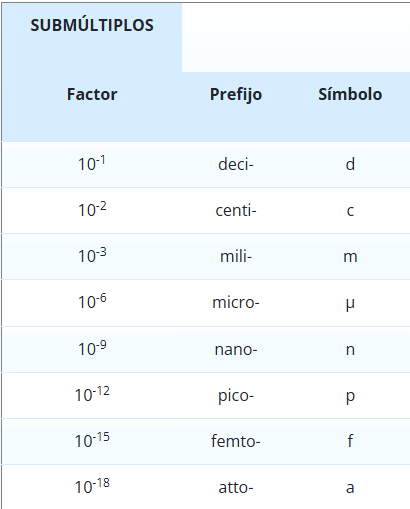
Prefijos y Factores
Al igual que con los múltiplos, los submúltiplos se identifican por medio de prefijos, que poseen sus respectivos símbolos. Adicionalmente posee un factor asignado al valor de la potencia de 10. Sin importar cual tipo unidad base se esté utilizando los submúltiplos siempre están en el mismo orden, siguiendo la imagen de la escalera.
- Deci-: Utiliza el símbolo d y su valor es de 10-1.
- Centi-: Con el símbolo c, con un factor de 10-2.
- Mili-: Usa el símbolo de m y utiliza el valor de 10-3.
- Micro-: Con el símbolo deµ y su factor es el de 10-6.
- Nano-: Su símbolo es n, su valor es de 10-9.
- Pico-: Utiliza como símbolo la p, usa el valor de 10-12.
- Femto-: Con símbolo f, usa el factor de 10-15.
- Atto-: Tiene como símbolo la a, con el valor del factor 10-18.
- Zepto-: Usa como símbolo la z y usa el factor 10-21.
- Yocto-: Su símbolo es la y, con el valor de 10-24.
Conversiones de Submúltiplos y Múltiplos
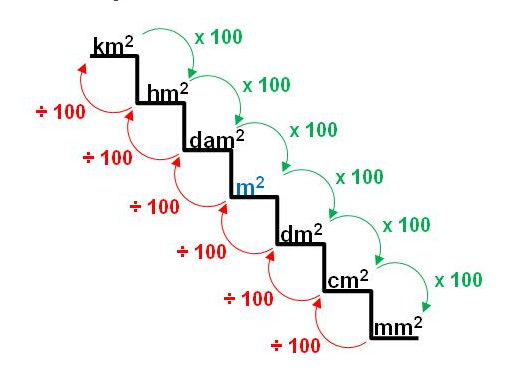
Recordemos que, para expresar cantidades muy grandes o muy pequeñas, se utilizan los múltiplos y los submúltiplos. Ambos se ubican dentro de una escalera, para facilitar de esta manera su conversión, al pasar de una unidad a otra.
Simulando de esta escalera se facilita visualmente el pasar de una unidad a otra, ubicando a los múltiplos en la parte superior y a los submúltiplos en la parte inferior. Para realizar esta conversión se utiliza la multiplicación y la división, tomando en cuenta la potencia de 10 de cada prefijo.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en líneaDesde este punto de vista si necesitamos pasar de un múltiplo a un submúltiplo se debe multiplicar según la potencia de 10 correspondiente. Por otra parte, si pasamos de un submúltiplo a un múltiplo se debe dividir por la correspondiente potencia de 10.
Los Submúltiplos de la Unidad de Volumen
De acuerdo con el Sistema Internacional de Medidas (SI), el metro cúbico (m³) es la unidad base del volumen. Como tal se pueden definir los submúltiplos de la siguiente manera:
- Metro Cubico (m³): Es considerada la unidad básica del volumen. Estaría posicionada en el centro de la escalera de conversiones.
- Decímetro cúbico (dm³): Ubicado un escalón por debajo de la unidad básica y equivale a una milésima parte de 1 metro cúbico (1 dm³ = 0.001 m³).
- Centímetro cúbico (cm³): Se encuentra dos escalones por debajo de la unidad base y su equivalencia es de una millonésima parte de 1 metro cúbico (1 cm³= 0.000001 m³).
- Milímetro cúbico (mm³): Esta en el tercer escalón por debajo de la unidad base y su valor corresponde a mil millonésimas partes de 1 metro cúbico (1 mm³= 0.000000001 m³).
Reglas para la Conversión
- Como primer paso se debe establecer con claridad cual es la unidad base que vamos a utilizar (litros, volumen, metros, entre otros).
- Se determinan los escalones a utilizar, tanto para subir (múltiplos), como para bajar (submúltiplos). Por lo general se utilizan solo 3 escalones tanto de subida como de bajada.
- Si se realiza una conversión desde una unidad mayor a una menor se multiplica por 10 la cantidad de escalones necesarios hasta llegar a la unidad que se quiere.
- Por otra parte, si se desea pasar de una unidad menor a una mayor se divide por 10 la cantidad de escalones hasta poder llegar a la unidad que se quiere.
Ejemplos de Conversiones de los Submúltiplos

Si queremos convertir o pasar de metros cúbicos a centímetros cúbicos, debemos multiplicar por 100, esto porque 1 m³ = 100 cm³. Si por otra parte se desea pasar de metros cúbicos a milímetros cúbicos se debe multiplicar por 1000 ya que 1 m³ = 1000 mm.
- Pasar de 5 metros cúbicos a centímetros cúbicos, debemos multiplicar 5 por 100 dando como resultado 500 cm³.
- Si pasamos de 3,2 metros cúbicos a milímetros cúbicos, se debe multiplicar por 1000 dando la operación de 3,2 x 1000= 3200 mm.
Utilizar los submúltiplos es la manera más sencilla y corta de expresar matemáticamente los números largos, complicando los cálculos de las medidas. Gracias a la potencia de 10 se pueden brindar los datos numéricos de manera más simple facilitando la realización de las medidas y formulas.









