La resta de fracciones es una operación matemática fundamental que consiste en determinar la diferencia entre dos fracciones. Este procedimiento permite obtener una fracción equivalente que representa el resultado de restar una cantidad fraccionaria de otra. A esta nueva fracción se le conoce (diferencia o simplemente resta). La operación requiere un análisis cuidadoso de las características de las fracciones involucradas, los denominadores, que pueden ser iguales o diferentes.
Símbolo o signo de la resta de fracciones
La resta de fracciones se identifica mediante el símbolo del guion o línea intermedia (-), conocido (menos). Este símbolo indica que una fracción se sustrae de otra para obtener una nueva fracción que refleja la diferencia entre ambas. Es universalmente reconocido en las matemáticas, (operador) que señala una disminución o sustracción. Su uso en las fracciones facilita expresar y resolver situaciones en las que se comparan o ajustan cantidades representadas de forma fraccionaria.

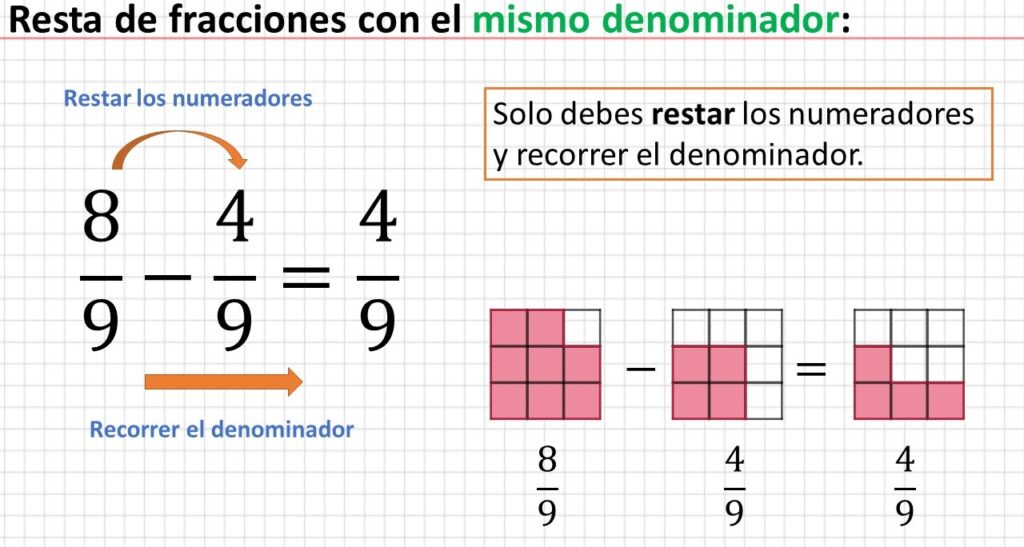
Resta de fracciones con el mismo denominador
La resta de fracciones puede parecer compleja, con práctica se vuelve sencilla. Las fracciones dependen tienen el mismo denominador o diferentes denominadores, los pasos son ligeramente diferentes. La resta de fracciones con el mismo denominador o resta de fracciones homogéneas es el procedimiento más simplificado y sencillo.
- Fracciones con el mismo denominador
- Ejemplo 1: 5/8 y 3/8
- 5 – 3= 2 el denominador queda igual 8
- La fracciones quedaría 2/8
- Simplificación: 2/8 se reduce a 1/4
- Ejemplo 2: 7/10 y 2/10
- 7 – 2= 5 el denominador queda igual 10
- La fracción quedaría 5/10
- Simplificación: 5/10 se reduce a 1/2
- Ejemplo 1: 5/8 y 3/8
Resta de fracciones con diferente denominador
La resta de fracciones con diferente denominador puede parecer un poco más compleja que la de fracciones con el mismo denominador, sigue un procedimiento lógico. Se pueden considerar dos métodos distintos para la resta de fracciones con diferente denominador, en este caso el primer método corresponde a la forma directa. No podemos obtener un mínimo común múltiplo del denominador y el método 2 corresponde a la obtención del mínimo común múltiplo.
- Pasos para restar fracciones con diferente denominador
- Ejemplo 1: 3/4 y 2/5
- Encuentra el MCM de los denominadores 4 y 5: El MCM de 4 y 5 es 20.
- Ajusta las fracciones al denominador común:
- Simplifica: La fracción 7/20 está en su forma más simple.
- Ejemplo 1: 3/4 y 2/5

La importancia de estas operaciones en matemáticas
La sustracción de fracciones es una operación matemática fundamental con una gran importancia en diversas áreas de la vida cotidiana y en el aprendizaje de conceptos matemáticos más avanzados. Incluir ejemplos concretos y ejercicios en el artículo ayudará a mostrar cómo estas operaciones están presentes en la vida cotidiana y en los estudios avanzados.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea- Base para el razonamiento matemático
- La sustracción de fracciones desarrolla habilidades críticas de la comprensión de denominadores comunes, el manejo de equivalencias y el orden lógico necesario p ara realizar cálculos correctos.
- Aplicaciones en la vida diaria
- Medición:
- En tareas de cocina o carpintería, a menudo se requiere restar fracciones
- Distribución de recursos:
- La comparación de porciones o cantidades e implica restar fracciones.
- Medición:
- Conexión con otros conceptos matemáticos
- La sustracción de fracciones no solo enseña a trabajar con números racionales
- Sirve de base para operaciones con números decimales.
- Refuerza el entendimiento de relaciones proporcionales.
- Prepara el terreno para resolver ecuaciones algebraicas.
- La sustracción de fracciones no solo enseña a trabajar con números racionales
- Relevancia en contextos científicos y técnicos
- Física y química:
- Los cálculos que involucran proporciones o concentraciones requieren trabajar con fracciones.
- Economía:
- Comparar porcentajes o índices en contextos financieros a menudo se traduce en restar fracciones.
- Física y química:
- Desarrollo del pensamiento lógico y abstracto
- Trabajar con fracciones, en la sustracción, mejora la capacidad de analizar problemas abstractos, una habilidad crucial para resolver situaciones no rutinarias.
La resta de fracciones es una habilidad matemática esencial que nos permite resolver problemas en la vida cotidiana y comprender conceptos más avanzados. Aprender a restar fracciones implica manejar términos de numerador, denominador y mínimo común múltiplo, de practicar operaciones básicas. y con dedicación y práctica, dominarás esta técnica, lo que te ayudará a fortalecer tus competencias matemáticas y a desarrollar un pensamiento lógico y analítico.









