Los triángulos o trígonos son figuras geométricas planas, básicas, que poseen tres lados en contacto entre sí en puntos comunes denominados vértices. Su nombre proviene del hecho de que posee tres ángulos interiores o internos, formados con un par de líneas en contacto en un mismo vértice. Estas figuras geométricas se nombran y clasifican de acuerdo a la forma de sus lados y al tipo de ángulo que construyen. Sus lados son siempre tres y la suma de todos sus ángulos siempre dará 180°.

En la historia del triángulo la antigüedad griega merece un lugar destacado. El griego Pitágoras (c. 569 – c. 475 a.C.) propuso su célebre teorema para los triángulos rectángulos, que reza que el cuadrado de la hipotenusa es igual a la suma del cuadrado de los catetos.

Propiedades del triángulo

La propiedad más obvia de los triángulos son sus tres lados, tres vértices y tres ángulos, que bien pueden ser semejantes o totalmente distintos entre ellos. Los triángulos son los polígonos más simples que hay, carecen de diagonal, y de tres puntos no alineados cualquiera puede formar un triángulo.

• Suma de los ángulos interiores
  • La suma de los ángulos interiores de un triángulo siempre es igual a 180 grados. Esta propiedad se cumple independientemente del tipo de triángulo.
• Lado más largo y ángulo mayor
  • En un triángulo, el lado más largo está siempre opuesto al ángulo más grande. De manera inversa, el lado más corto está opuesto al ángulo más pequeño.
• Desigualdad triangular
  • La suma de las longitudes de dos lados de un triángulo siempre es mayor que la longitud del tercer lado.
    • Matemáticamente: a + b > c,a + c > b,b + c > a
• Clasificación x lados
  • Equilátero: Tiene los tres lados iguales y sus ángulos internos miden 60 grados.
    • Isósceles: Tiene dos lados iguales y dos ángulos internos iguales.
      • Escaleno: Tiene los tres lados y los tres ángulos diferentes.
• Clasificación x ángulos
  • Acutángulo: Los tres ángulos son agudos (menores de 90°).
    • Rectángulo: Uno de los ángulos es recto (90°).
      • Obtusángulo: Uno de los ángulos es obtuso (mayor de 90°).
• Altura, mediana y bisectriz
  • Altura: Segmento perpendicular trazado desde un vértice al lado opuesto (o su extensión).
    • Mediana: Segmento que une un vértice con el punto medio del lado opuesto.
      • Bisectriz: Segmento que divide un ángulo del triángulo en dos ángulos iguales.

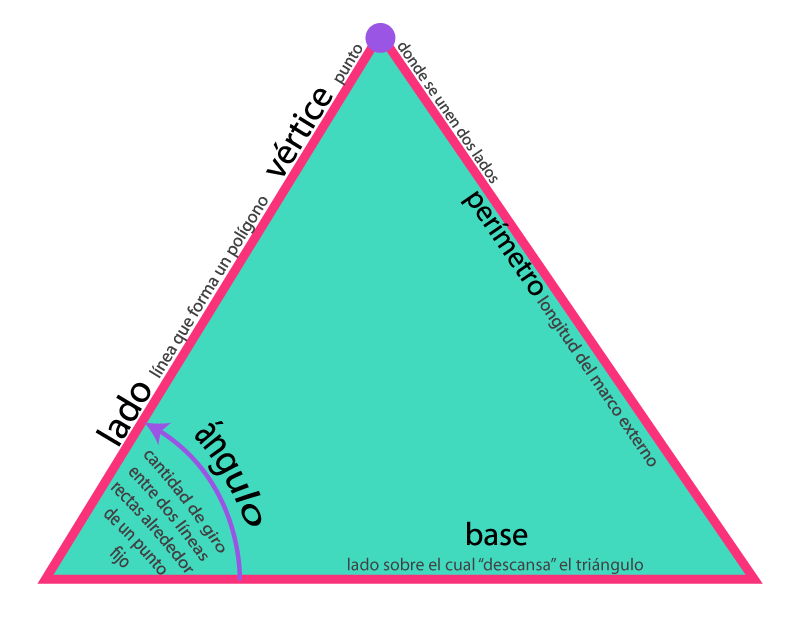
¿Cuáles son los elementos de los triángulos?

Los elementos del triángulo son los que componen esta figura geométrica, los cuales se pueden definir en elementos primarios y secundarios. Los elementos primarios son los vértices, lados y ángulos (interiores y exteriores).

• Elementos primarios
  • Estos son los elementos básicos que constituyen la figura del triángulo:
  • Vértices
    • Un triángulo siempre tiene tres vértices, que se nombran comúnmente con letras mayúsculas (A, B, C).
  • Lados
    • Son los segmentos de recta que unen los vértices del triángulo.
    • Un triángulo tiene tres lados y su longitud determina el tipo de triángulo (equilátero, isósceles o escaleno).
  • Ángulos interiores
    • Son los ángulos formados x dos lados consecutivos del triángulo en cada vértice.
    • La suma de los tres ángulos interiores es siempre igual a 180 grados.
  • Ángulos exteriores
    • Son los ángulos formados en un lado del triángulo y la prolongación del lado adyacente.
    • Cada ángulo exterior es suplementario al ángulo interior correspondiente (180°−ángulo interior).
• Elementos secundarios
  • Estos elementos no definen el triángulo, se derivan de los elementos primarios y son fundamentales para resolver problemas geométricos:
  • Alturas
    • Segmentos perpendiculares trazados desde un vértice hasta el lado opuesto o su prolongación.
    • Medianas
      • Segmentos que van desde un vértice hasta el punto medio del lado opuesto.
      • Las tres medianas se intersectan en el baricentro, que divide cada mediana en una relación de 2:1
    • Bisectrices
      • Rectas que dividen un ángulo interior del triángulo en dos partes iguales.
      • Las bisectrices se intersectan en el incentro, que es el centro de la circunferencia inscrita.
    • Mediatrices
      • Rectas perpendiculares trazadas desde los puntos medios de los lados.
    • Circuncentro e incentro
      • El circuncentro es el punto equidistante de los vértices, el incentro es el punto equidistante de los lados.

¿Qué tipos de triángulos existen?

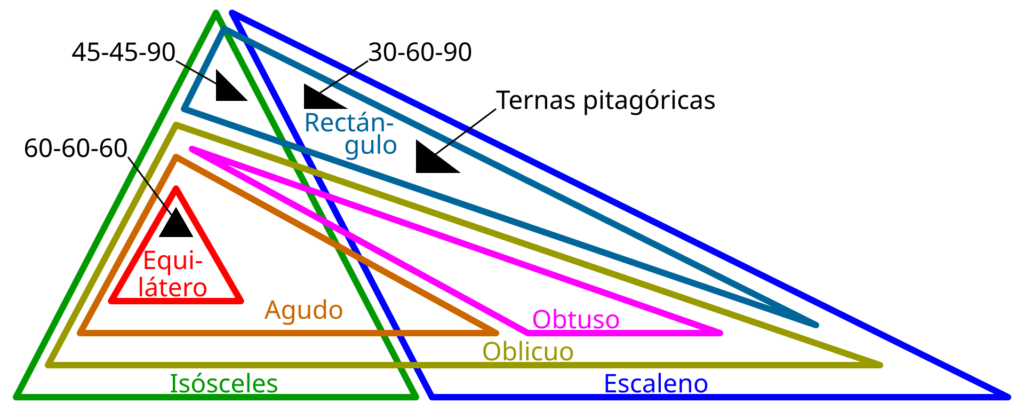
Los triángulos se clasifican según sus lados en equiláteros, isósceles y escalenos y según sus ángulos en acutángulos, rectángulos y obtusángulos. Cada tipo tiene características únicas que los distinguen en geometría.

• Según la longitud de sus lados
  • Triángulo equilátero
    • Tiene tres lados iguales.
      • Todos sus ángulos interiores son iguales, cada uno de 60°.
  • Triángulo isósceles
    • Tiene dos lados iguales y uno desigual.
      • Los ángulos opuestos a los lados iguales, son iguales.
  • Triángulo escaleno
    • Tiene los tres lados desiguales.
      • Sus tres ángulos interiores son diferentes.
• Según sus ángulos interiores
  • Triángulo acutángulo
    • Tiene tres ángulos agudos, menores de 90°.
      • Los lados de un triángulo rectángulo se llaman:
    • Hipotenusa: El lado opuesto al ángulo recto (el más largo).
    • Catetos: Los lados que forman el ángulo recto.
  • Triángulo obtusángulo
    • Tiene un ángulo obtuso, es mayor de 90°.
      • Los otros dos ángulos son agudos.

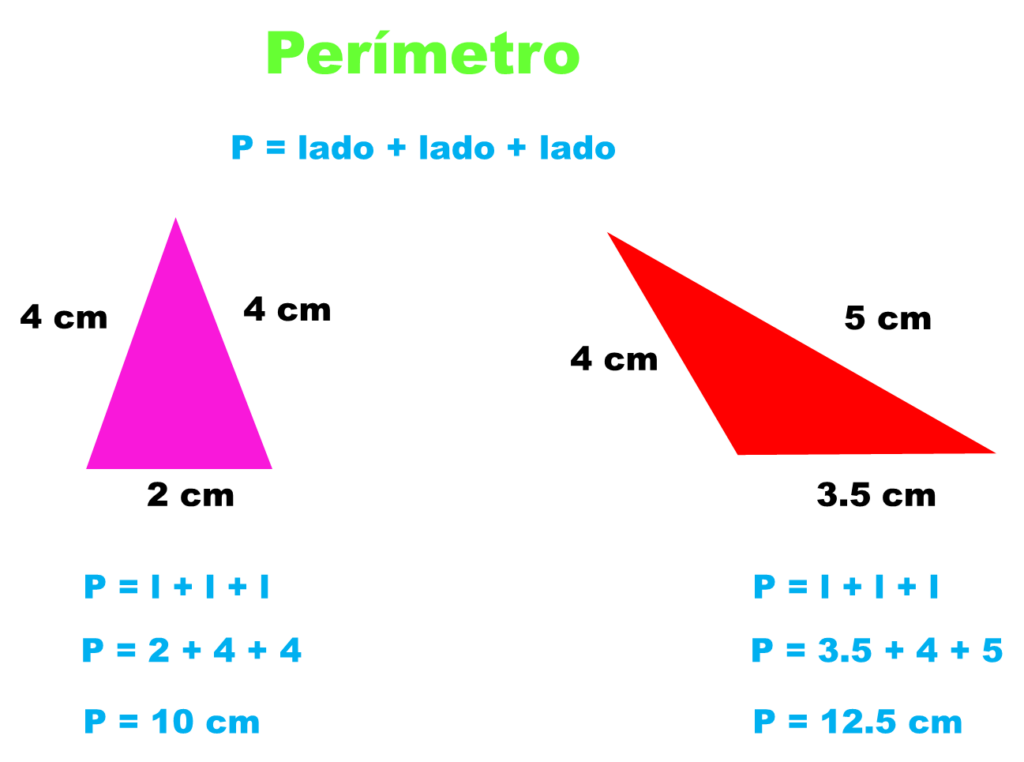
Perímetro

El perímetro de un triángulo es la suma de la longitud de sus lados y suele denotarse con la letra (p) o con (2s). La ecuación para determinar el perímetro de un triángulo ABC determinado es: Perímetro = L 1​ + L 2 ​+ L 3

• Pasos para calcularlo
  • Identificar los lados del triángulo:
    • Asegúrate de conocer la medida de cada lado (L 1​, L 2, L 3)
  • Sumar las longitudes:
    • Suma las tres medidas para obtener el perímetro.
• Ejemplo:
  • Un triángulo tiene lados de 5 cm, 7 cm y 10 cm, su perímetro es:
    • Perímetro = 5 cm + 7 cm + 10 cm = 22 cm.
  • Esta fórmula aplica para cualquier triángulo, independientemente de su tipo.

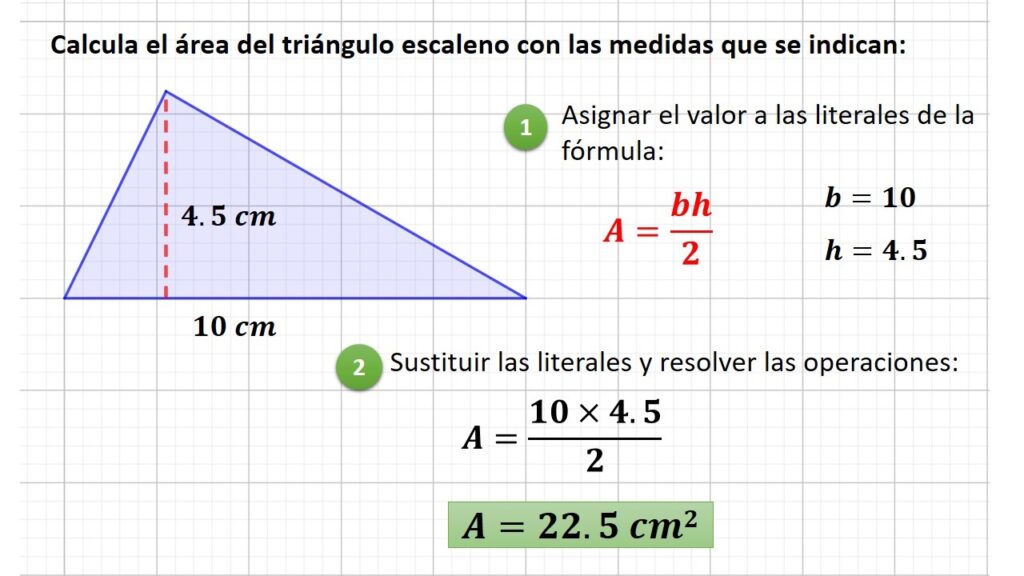
Área

El área de un triángulo (a) es el espacio interior delimitado x sus tres lados. Puede calcularse sabiendo su base (b) y su altura (h), de acuerdo a la fórmula: Área = base × altura entre 2

• Pasos para calcular el área
  • Identificar la base (b):
    • Es uno de los lados del triángulo que se toma en referencia.
  • Determinar la altura (h):
    • Es la distancia perpendicular desde el vértice opuesto a la base hasta la base misma.
• Sustituir los valores en la fórmula.
  • Ejemplo:
    • Un triángulo tiene una base de 8 cm y una altura de 5 cm, su área se calcula.
      • Área = 28 cm × 5 cm ​= 40 cm² ​= 20 cm².

Los triángulos son figuras geométricas esenciales que se encuentran en la naturaleza, el arte y la arquitectura. Su clasificación según lados y ángulos permite un análisis detallado, proporcionando herramientas para resolver problemas geométricos complejos. Entender sus propiedades fomenta habilidades de razonamiento lógico y matemático, esenciales en diversas disciplinas. Su estudio fomenta la apreciación de cómo la geometría impacta nuestro entorno cotidiano, desde el diseño de estructuras hasta la creación de patrones artísticos. Explorar los triángulos no solo amplía el conocimiento matemático, revela la profunda conexión entre las matemáticas y el mundo que nos rodea.