Las pirámides son figuras geométricas con una base en forma de polígono, con caras laterales triangulares y se unen en un mismo vértice. Es una estructura geométrica tridimensional con forma de cono truncado y de base plana. La base de una pirámide puede ser cualquier polígono, un triángulo, un cuadrado, un pentágono, etc. y el vértice de la pirámide se llama ápice. Su altura es la distancia perpendicular desde el vértice hasta el plano que contiene la base.

Definición de las pirámides geométricas

Se llama pirámide a un cuerpo geométrico que es la unión de todos los segmentos que unen todos los puntos de un polígono (S) con un punto (P) exterior al plano del polígono. Considerando que el polígono es una parte del plano y es un conjunto bidimensional.

• Características principales
  • Base:
    • Es un polígono plano, que puede ser de cualquier tipo, un triángulo, cuadrado, pentágono, etc.
  • Caras laterales:
    • Son triángulos que tienen un lado común con la base y comparten el vértice de la pirámide.
  • Vértices:
    • Incluyen los vértices de la base y el vértice superior donde convergen las aristas laterales.
  • Altura:
    • Es la distancia perpendicular entre el vértice de la pirámide y el plano de la base.
• Clasificación
  • Según la forma de la base:
    • Pirámide triangular (base de tres lados).
    • Pirámide cuadrangular (base cuadrada o rectangular).
    • Pirámide pentagonal (base de cinco lados), etc
• Ejemplos en la vida real
  • Las pirámides de Egipto, la Gran Pirámide de Giza, son ejemplos arquitectónicos de pirámides cuadrangulares.
  • Los tepees o tiendas cónicas tradicionales de los nativos americano. Tienen una estructura similar a una pirámide con base circular (técnicamente son conos).

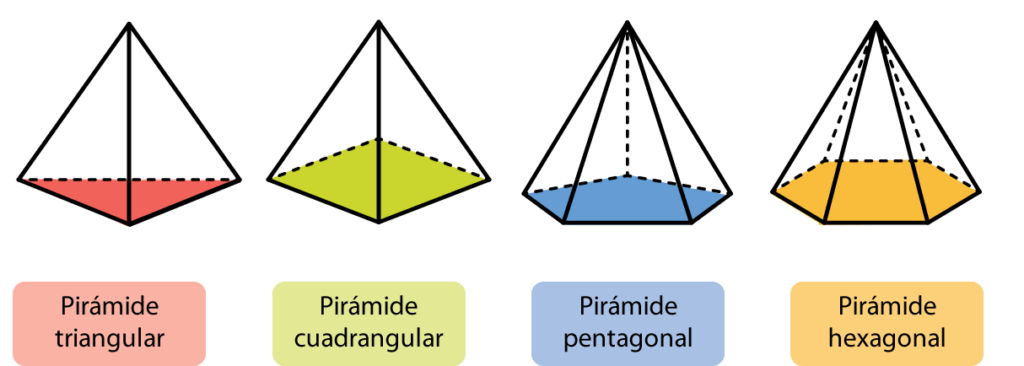
Tipos de pirámides

Solo existen tres pirámides de este tipo: el tetraedro (pirámide triangular), la pirámide cuadrada y la pirámide pentagonal. Una pirámide convexa tiene de base un polígono convexo. La pirámide cóncava tiene de base un polígono cóncavo.

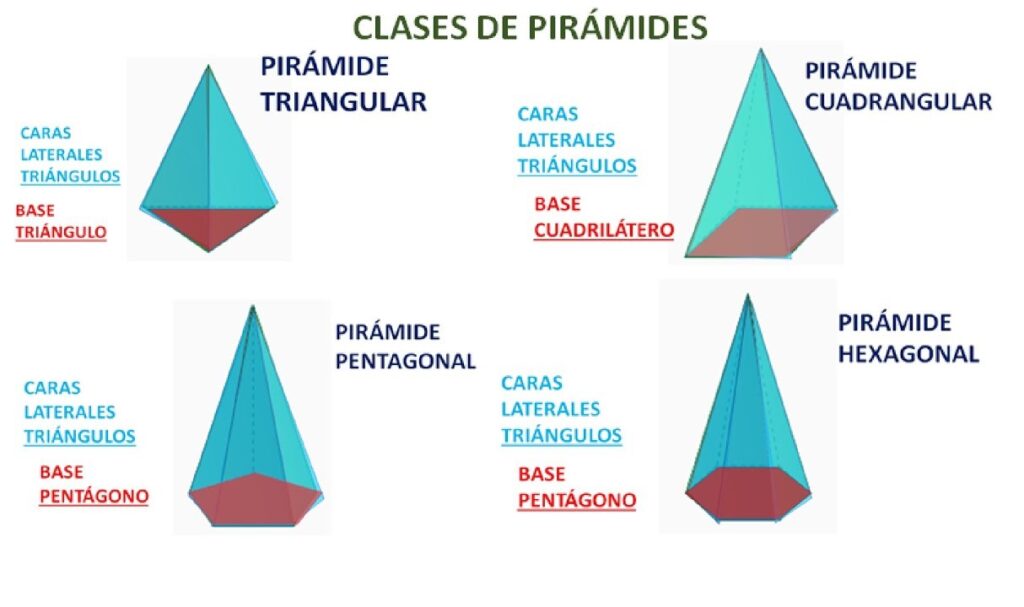
• Según la forma de la base
  • La forma del polígono en la base determina el nombre de la pirámide:
    • Pirámide triangular:
      • La base es un triángulo. Este tipo de pirámide tiene 4 caras (1 base y 3 caras laterales).
    • Pirámide cuadrangular:
      • La base es un cuadrado o un rectángulo. Tiene 5 caras (1 base y 4 caras laterales).
    • Pirámide pentagonal:
      • La base es un pentágono. Tiene 6 caras (1 base y 5 caras laterales).
    • Pirámide hexagonal:
      • La base es un hexágono. Tiene 7 caras (1 base y 6 caras laterales).
• Según su regularidad
  • Pirámide regular:
    • La base es un polígono regular (todos sus lados y ángulos son iguales).
    • Las caras laterales son triángulos isósceles congruentes.
    • Ejemplo: una pirámide con base cuadrada y caras laterales idénticas.
  • Pirámide irregular:
    • La base es un polígono irregular (sus lados y ángulos no son iguales).
    • Las caras laterales pueden ser triángulos diferentes.
    • Ejemplo: una pirámide con base rectangular de lados desiguales.
• Según la posición del vértice
  • Pirámide recta:
    • El vértice está directamente alineado sobre el centro de la base (en perpendicular).
    • Todas las caras laterales son triángulos isósceles.
  • Pirámide oblicua:
    • El vértice no está alineado con el centro de la base, lo que hace que la pirámide se incline.
    • Las caras laterales son triángulos escaleno de diferentes tamaños.
• Según la dimensión de la base:
  • Pirámide truncada:
    • Se obtiene al cortar una pirámide con un plano paralelo a su base, eliminando la parte superior.
    • El resultado es un sólido con dos bases: la original y una más pequeña.

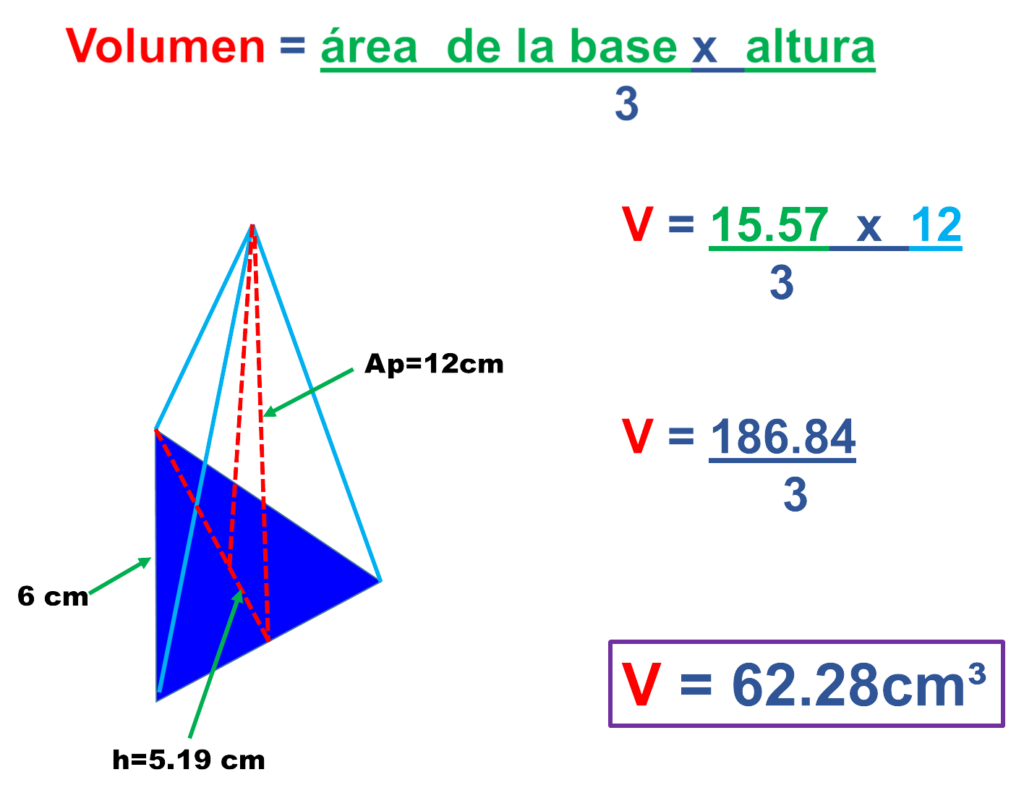
¿Cuál es la fórmula área y volumen?

• Área de una pirámide
  • El área total (Atota l) de una pirámide incluye el área de su base y el área de sus caras laterales.
    • Fórmula general: Atotal​ = Abase​ + Alateral
  • Componentes:
    • Área de la base (Abase): Depende de la forma del polígono base
      • Un cuadrado: Abase= l² (lado al cuadrado).
      • Es un triángulo: Abase = ½ ⋅ b ⋅ h (base x altura entre dos).
      • Un polígono regular: Abase = ½ ⋅ P ⋅ a, donde P es el perímetro y a es el apotema
  • Área lateral (Alateral): La suma del área de las caras laterales. Las caras laterales son triángulos iguales.
    • Alateral ​= ½ ⋅ Pbase ​⋅ hlateral​
  • Donde Pbase es el perímetro de la base y hlateral​ es la altura de las caras laterales (apotema lateral).
• Volumen de una pirámide:
  • El volumen (V) de una pirámide se calcula, un tercio del producto del área de la base y la altura perpendicular de la pirámide.
    • Fórmula: V = ⅓ ​⋅Abase ​⋅ h
      • Abase​: Área de la base (según su forma).
      • h: Altura perpendicular desde el vértice al plano de la base.
  • Ejemplo práctico:
    • Para una pirámide cuadrangular recta con base de lado l y altura h
      • Abase​ = l²
      • Alatera l ​= 2 ⋅ l ⋅ hlateral​ (hlatera es la altura de las caras laterales).}
        • V = ⅓ ​⋅l2 ⋅ h
• Aplicaciones:
  • Estas fórmulas son útiles en arquitectura, ingeniería y diseño.
  • Se utilizan en cálculos de volúmenes de estructuras, pirámides y techos inclinados.

Histórica de las pirámides al desarrollo matemático

Las pirámides han sido fundamentales en el desarrollo matemático, particularmente en la geometría y la ingeniería. Las grandes pirámides de Egipto, la de Keops, muestran un dominio avanzado de las proporciones, la simetría y la medición precisa. Los antiguos egipcios usaron fórmulas aproximadas para calcular áreas y volúmenes, precursores del conocimiento matemático moderno. En Mesoamérica, las pirámides de Chichén Itzá reflejan un entendimiento profundo de la astronomía y la matemática aplicada. Estos monumentos inspiraron el estudio de los sólidos geométricos, sentando bases para la trigonometría y las proporciones, influyendo en la arquitectura y la matemática contemporáneas.

Las pirámides son figuras geométricas fascinantes que combinan simplicidad y complejidad. Sus bases poligonales y caras triangulares convergen en un vértice, creando estructuras únicas con aplicaciones prácticas y teóricas. Desde las pirámides egipcias hasta diseños modernos en ingeniería y arquitectura, estas formas ilustran la belleza y utilidad de las matemáticas en nuestra vida diaria.