El concepto de geometría nos indica que se trata de una rama de las matemáticas, en la cual se estudian las medidas y las propiedades de las figuras geométricas. Analiza cada una de las figuras según sus líneas, puntos, superficie, diseño y ángulos, los cuales permiten su aplicación en áreas como la arquitectura, diseño o cartografía.

Considerada como una de las ramas más antiguas, la geometría se constituye en base a los conocimientos del volumen, área, perímetro y longitudes de los objetos. Utilizada desde la cultura Babilónica o en el antiguo Egipto, se desarrollo el estudio de la circunferencia, el numero π y el sistema hexagonal.

Adicionalmente se inicio el uso de la fórmula de cálculo para las propiedades de las figuras geométricas. Así como la incorporación de la cartografía, la astronomía, la geometría analítica y de ecuaciones que marcaría una nueva época en este campo.

Matemáticos como René Descartes, Gauss, Euler, Diodoro Sículo, Euclides o Estrabón fueron los encargados de revolucionar la geometría a través del tiempo.

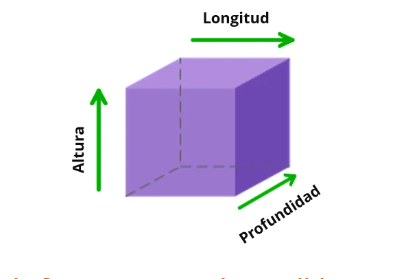
Tipos de Propiedades de las Figuras Geométricas

Al estudiar cada una de las propiedades de las figuras geometrías, se debe comprender que hay diferentes clasificaciones para ellas. Cada clasificación se basa en características que las unen como grupo y que las diferencian al mismo tiempo de las demás.

Las propiedades se pueden clasificar por su dimensión, por sus características comunes y por otras propiedades. Cada una de las características permiten identificar y definir el tipo de figura con la que estemos trabajando.

Propiedades por Dimensión

• Adimensional: Son aquellas figuras que No poseen ninguna (0) dimensión. En este caso el punto (.) es la única figura que cumple con esta propiedad, ya que no posee altura, ancho o longitud.
• Unidimensional: Se refiere a las figuras que poseen una sola (1) dimensión. Ejemplo el segmento, la recta o semirrecta, ya que solo poseen longitud y carecen de altura y achura.
• Bidimensional: También conocidas como figuras planas, son las que tienen dos (2) dimensiones. Estas figuras solamente poseen ancho y longitud, como es el caso del círculo, la elipse o un polígono.
• Tridimensional: Comúnmente se le conoce como cuerpos sólidos, sus figuras se encuentran en tercera (3) dimensión. En esta categoría podemos encontrar al cubo, esferas, poliedro o cilindro, los cuales poseen anchura, altura y longitud.

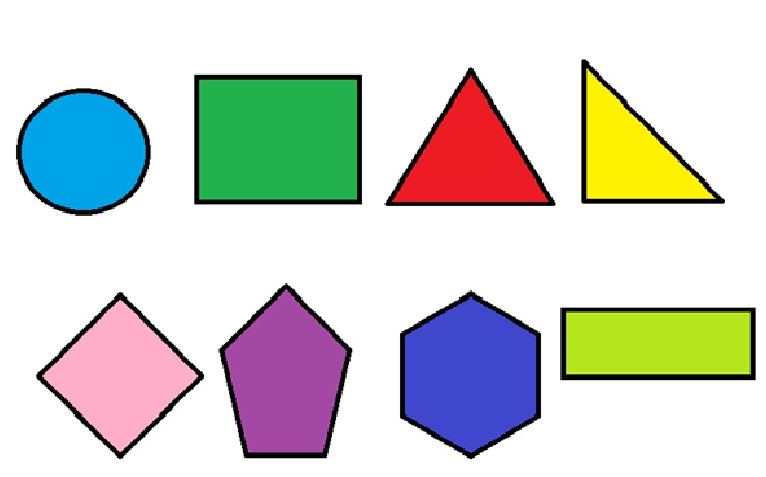
Propiedades Comunes

• Perímetro: Corresponde a la medida de la totalidad de los bordes que se encuentran en cada figura.
• Área: Se refiere a la totalidad del espacio bidimensional que se encuentra dentro de la figura geométrica.
• Ángulos: Es la medida que obtiene la rotación que se encuentra entre dos bordes o líneas que se unen en el vértice.
• Volumen: Se refiere al espacio tridimensional que esta dentro de una figura geométrica.
• Vértices y Lados: Son los puntos y líneas rectas que conforman las figuras.

Propiedades de las Figuras Tridimensionales

• Vértices: Son los puntos en donde se unen las aristas.
• Caras: Corresponde a la superficie plana que se encuentra en un cuerpo geométrico.
• Aristas: Se refiere a las líneas ubicadas en las caras de las figuras.

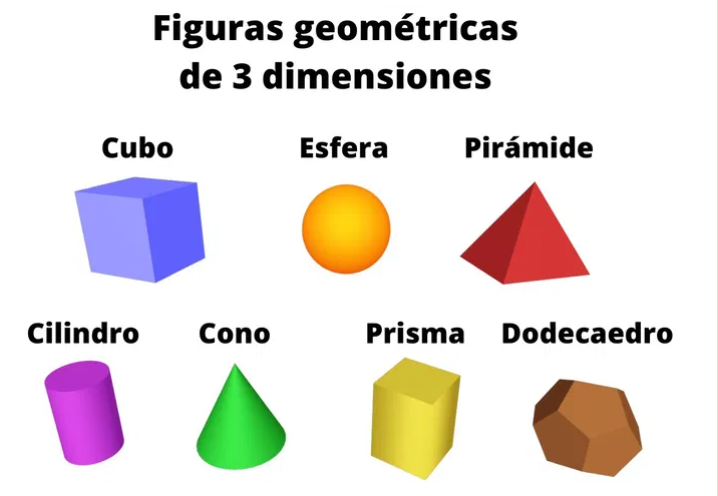
Otras Propiedades de las Figuras Geométricas

• Simetría: Se refiere a las figuras geometrías que son exactamente iguales, en todos los aspectos, propiedades y características.
• Regularidad: Esta propiedad se puede dividir en regular o regular.
  • Regular: Se da en una figura cuyos ángulos y lados son regulares o iguales. Como por ejemplo el triángulo equilátero.
  • Irregular:  Se presenta en figuras cullos lados y ángulos no son iguales. Ejemplo, los triángulos isósceles y escalenos.
• Congruencia: Corresponde a aquellas figuras que poseen características iguales, pero no son idénticas. Ejemplo dos figuras que poseen la misma forma, pero distinto tamaño.
• Limite, Exterior e interior: El espacio que se encuentra dentro de una figura se le conoce como interior, mientras que al espacio que esta fuera de ella se le llama exterior. A la línea que separa ambos espacios se le denomina como límite.
• Longitud de los vértices: Referente a la medida de la longitud de cada segmento que conforma una figura geometría.

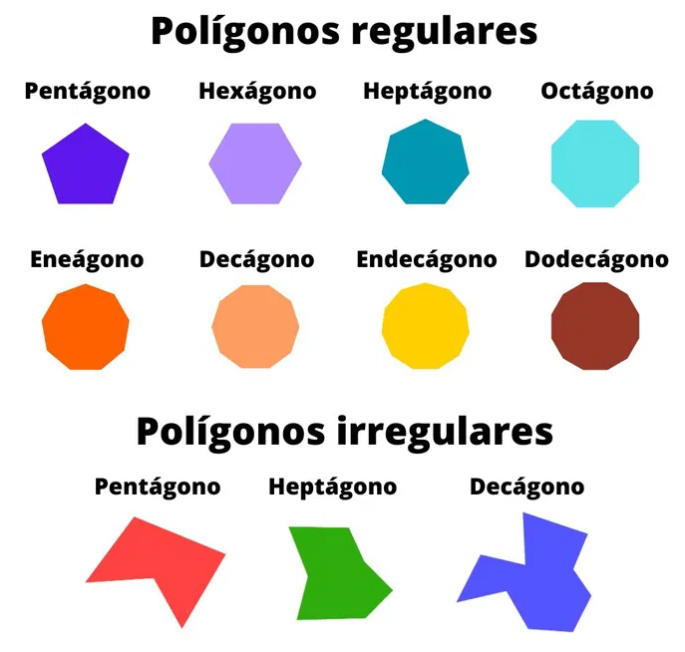
Importancia de las Propiedades de la Figuras Geométricas

Cada una de las figuras geometrías con vitales para que se pueda desarrollar el pensamiento espacial y lógico a la hora de resolver problemas prácticos. Las propiedades de las figuras geométricas permiten identificar cada una de las figuras, su utilización y la manera de calcular sus volúmenes, perímetros u áreas.

El uso que se le da a las figuras permiten el razonamiento grafico creativo en campos como la arquitectura, informática, diseño, cartografía, robótica, entre muchas otras. Adicionalmente un buen conocimiento de las figuras nos da una mejor comprensión del entorno que nos rodea, así como poder comparar, modelar, clasificar, describir e identificar diversos objetos.