Se puede definir a los ángulos como una figura que se forma gracias a dos líneas o semirrectas que comparten el mismo vértice (punto final). Cuando se habla de la medida de los ángulos, se hace a partir de la amplitud que existe en el arco de la circunferencia que se centra en el vértice que comparten las semirrectas.
Comúnmente a los ángulos se le miden por medio de los grados o radianes. Los grados o también llamado grado de arco, corresponde a la medida de un ángulo plano. Dentro de una rotación completa, de un círculo, el cual se conforma por 360 grados. Su símbolo es el ° y se coloca al final del valor numérica.
El radian por su parte es representado con el símbolo de rad. Se define como la medida del ángulo con vértice en el centro de un círculo. Sus lados están cortados por el arco de la circunferencia, que además posee igual medida que el radio.
La Medición de los Ángulos
Para poder realizar la medición de un ángulo es necesario trazar un arco de circunferencia, el cual esta centrado en el vértice. Esta tarea se utiliza un instrumento conocido como compás, el cual es usado para trazar arcos o círculos. También se le puede utilizar para medir distancias, por ejemplo, en los mapas, en la navegación, en las matemáticas y en el dibujo técnico.
Al tomar el cociente de la longitud “s” del arco de la circunferencia y multiplicarlo por el radio “r”, da como resultado el radian “rad” del ángulo. Igualmente, dicha ecuación puede ser representada de la siguiente manera θ = 2/r = rad.
En caso de que el ángulo deba ser expresado en alguna otra unidad angular, el resultado se obtiene al multiplicar el ángulo por la constancia de conversión k/2π. El símbolo de “k” representa a la totalidad de grados en un círculo, en este caso k = 360°. Es importante anotar que el valor del ángulo, no depende del tamaño del círculo, ya que, si la medida del radio cambia, la medida del arco lo hace en la misma proporción.
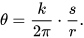
Las Diferentes Unidades Angulares
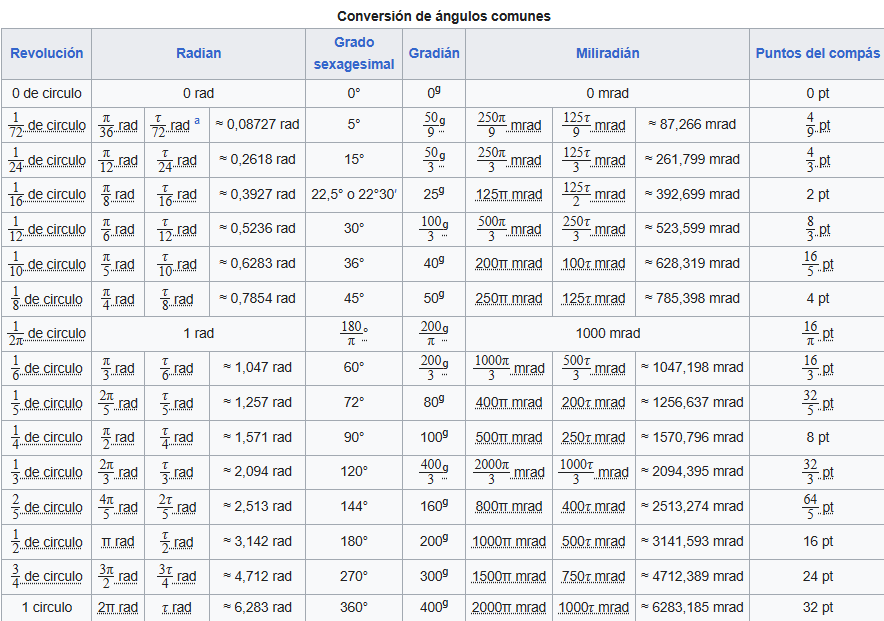
Existe una gran variedad de unidades que se pueden utilizar para representar la medida de los ángulos. Tanto el grado como el radian son las unidades más comúnmente usadas, pero existen otras que veremos a continuación, ordenadas de mayor a menor magnitud en cuanto a valores.
- Giro: Llamada de esta manera ya que representa a un giro completo del círculo, utiliza los símbolos de “cyc”, “rev” o “rot”, según el valor de la aplicación. Se representa como n=1.
- Cuadrante: Representa la cuarta parte de un círculo, n=4 y es usado generalmente para los ángulos rectos de 90°.
- Sextante: Usada en valores de 1/6 del giro total de un círculo, se representa como n=6.
- Radian: n=2.
- Ángulo horario: Corresponde a 1/24 del total de una vuelta del círculo (n=24).
- Puntos del compás: Es el más utilizado para la navegación y es representado como n=32.
- Hexacontada: Equivale a 6° (n=60), lo que quiere decir que una vuelta entera del circulo se divide en 60 hexacontadas.
- Pechus: Posee un valor de 2°.
- Grado binario: También conocido como radian binario y se representa como n=256.
- Grado: n=360.
- Parte del diámetro: Su valor corresponde a 1/60 de un radián.
- Grad: Representado como n=400, también se le conoce como gradian, gonio o gon.
- Milirradio: Corresponde a la milésima parte de un radian.
- Arcominuto: También se le conoce como minuto de arco y representa 1/60 de un grado.
- Arcosegundo: Su valor corresponde a 1/60 de un arcominuto, por lo que seria 1/360 de un grado.
- Miliarcosegundo: Se le conoce más comúnmente por su abreviación “mas” y es utilizado generalmente en astronomía.
- Microarcosegundo: Su abreviación es la de “µas”, empleado generalmente en las mediciones de alta precisión.
Los Tipos de Ángulos
Dentro de un circulo se pueden presentar diversos tipos de ángulos, estos varían según la medida de los grados que cada uno posee. En geometría un ángulo se puede definir como la amplitud que existe entre dos líneas, siempre y cuando ambas inicien en el mismo punto.
La manera más sencilla de identificar un ángulo es por medio de la utilización del Transportador de ángulos. Este instrumento se encarga de identificar en grados, la medida entre las dos líneas, en otras palabras, indica la medida en grados de los ángulos, pudiendo de esta manera identificar rápidamente que tipo de ángulo se está usando.
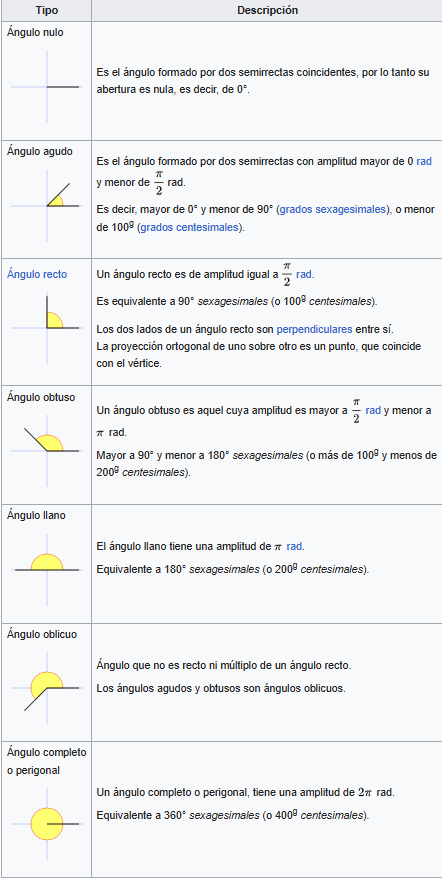
Un ángulo geométrico puede caracterizarse por su magnitud ya que, con la menor rotación de uno de sus rayos, su medida cambia completamente. Dentro de un circulo se pueden dar un sinfín de ángulos, ya sean de la misma medida (congruentes) o de distintos grados.
Ya sea por medio de grados o radianes, las unidades de los ángulos, dependen en gran medida de la utilización del área que le esté utilizándolo. Pero comúnmente cuando se usan los radianes es porque son adimensionales y se utilizan en el análisis dimensional (herramienta para simplificar cualquier fenómeno).









