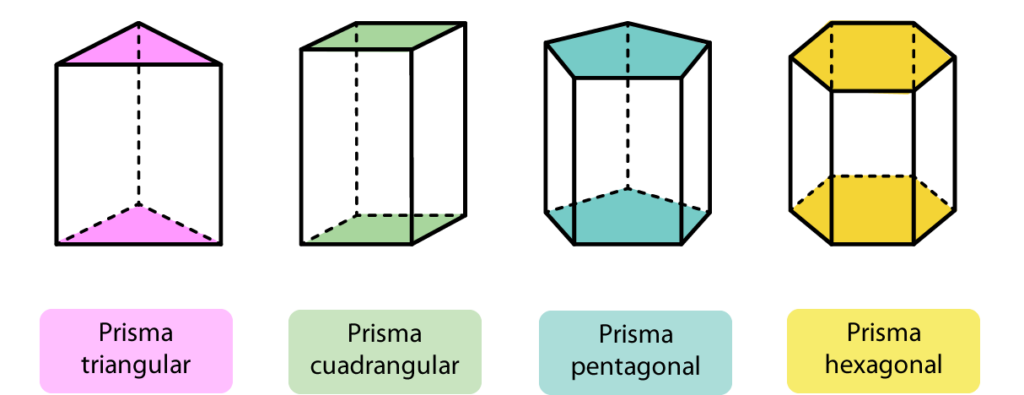
En geometría los prismas son un poliedro que tiene dos bases congruentes y paralelas, acompañadas de caras laterales en forma de paralelogramos. Se clasifica y nombra según la forma de sus bases. Los prismas pertenecen a una subclase de poliedros llamada prismatoides, la cual agrupa figuras tridimensionales que tienen dos bases paralelas y caras laterales que pueden variar en forma.
Características principales de los prismas
Los prisma son un sólido geométrico que tiene dos bases paralelas e iguales. Que pueden ser de cualquier forma poligonal y sus caras laterales son siempre paralelogramos. Estas caras unen los lados correspondientes de las bases, creando una estructura tridimensional uniforme.
- Bases paralelas y congruentes
- Las bases son polígonos idénticos y están ubicadas en planos paralelos.
- El tipo de polígono que forma las bases determina el nombre del prisma (ejemplo, las bases son triángulos, se llama prisma triangular).
- Caras laterales
- Las caras laterales son paralelogramos (rectángulos, el prisma es recto).
- El número de caras laterales es igual al número de lados del polígono base.
- Aristas y vértices:
- Un prisma tiene aristas laterales que conectan los vértices de las bases.
- La cantidad total de vértices y aristas depende del tipo de polígono base.
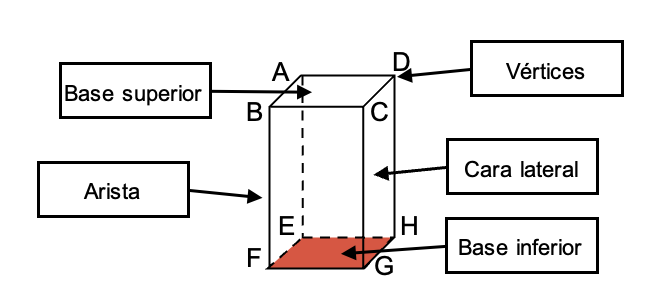
¿Qué tipos de prismas existen?
Existen diversos tipos de prismas su clasificación se basa en aspectos fundamentales, la forma de sus bases, la disposición de sus caras laterales y la regularidad de las bases. Esta clasificación resulta esencial para comprender las propiedades y características geométricas de cada prisma, se aplica en conceptos y problemas matemáticos, arquitectónicos o científicos.
- Clasificación según la forma de las bases
- La forma del polígono que constituye las bases define el tipo de prisma.
- Prisma triangular:
- Sus bases son triángulos, lo que le otorga tres caras laterales.
- Prisma cuadrangular:
- Tiene bases cuadriláteras, cuadrados o rectángulos y cuatro caras laterales.
- Prisma pentagonal:
- Sus bases son pentágonos, lo que genera cinco caras laterales.
- Prisma hexagonal:
- Las bases son hexágonos, con seis caras laterales.
- Prismas poligonales:
- Incluyen aquellos prismas cuyas bases son polígonos con más de seis lados, los heptágonos, octógonos, etc.
- Clasificación según la disposición de las caras laterales
- Prisma recto:
- Las caras laterales son rectángulos.
- Los bordes verticales del prisma son perpendiculares a las bases.
- Prisma oblicuo:
- Las caras laterales son paralelogramos que no forman ángulos rectos con las bases.
- La altura del prisma no coincide con la longitud de los bordes verticales.
- Prisma recto:
- Clasificación según la regularidad de las bases
- La regularidad o irregularidad de las bases, influye en el tipo de prisma
- Prisma regular:
- Sus bases son polígonos regulares, figuras con lados y ángulos iguales.
- Ejemplo: prismas con bases cuadradas o hexagonales regulares.
- Prisma irregular:
- Las bases son polígonos irregulares, donde los lados o ángulos no son iguales.
- Este tipo de prisma es menos común, aparece en estructuras más complejas.
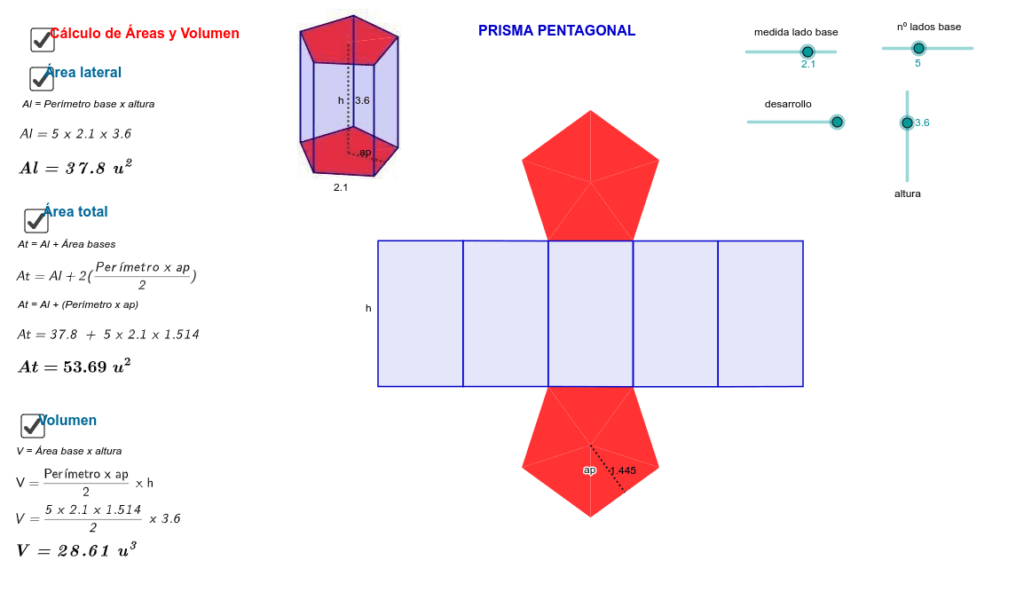
¿Cuál es la fórmula para calcular áreas y perímetros?
Para calcular las áreas y perímetros de los prismas, se deben conocer algunos aspectos clave de la figura, la base del prisma y su altura. Dependiendo de la forma de la base, las fórmulas se ajustan, estos son los principios generales para calcular áreas, perímetros y volumen de prismas.
- Área superficial del prisma: La fórmula general para calcular el área superficial de un prisma es
- A=2B+P⋅h
- Perímetro de la base del prisma: El perímetro de la base (P) depende de la forma de la base del prisma. Para un prisma con base poligonal (un prisma rectangular, triangular, hexagonal, etc.), el perímetro es simplemente la suma de las longitudes de todos los lados de la base.
- • En el caso de un prisma rectangular, el perímetro de la base se calcula:
P=2(l+w)
- • En el caso de un prisma rectangular, el perímetro de la base se calcula:
- Volumen del prisma: El volumen de un prisma se calcula multiplicando el área de la base x la altura.
- V=B⋅h
- donde:
- V es el volumen del prisma.
- B es el área de la base.
- h es la altura del prisma.
- donde:
- V=B⋅h
La importancia de la geometría en matemáticas
La geometría es una de las ramas fundamentales de las matemáticas, encargada de estudiar las formas, las posiciones relativas de los objetos en el espacio y sus propiedades. Su relevancia trasciende el ámbito teórico, tiene aplicaciones prácticas en múltiples disciplinas, la física, la ingeniería, la arquitectura, el arte y la tecnología. La geometría permite desarrollar una comprensión profunda de las formas y estructuras que nos rodean. A través del análisis de figuras bidimensionales (círculos y triángulos) y tridimensionales (prismas y esferas), los estudiantes adquieren habilidades espaciales esenciales para resolver problemas visuales y prácticos.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en líneaLos prismas en geometría no solo son una herramienta para entender el mundo físico, es una disciplina que impulsa el desarrollo del pensamiento crítico, la creatividad y la innovación. Su importancia en las matemáticas y en la vida práctica demuestra que es una pieza esencial para la comprensión de nuestro entorno y la resolución de desafíos complejos.









