En el campo de las matemáticas, se le llama potencias a una relación aritmética entre dos términos. Una base (a) y un exponente (n), de manera tal que la base se multiplica una cantidad de veces, lo que el exponente indique. Estas mismas son una manera abreviada de escribir una multiplicación formada en varios números iguales.

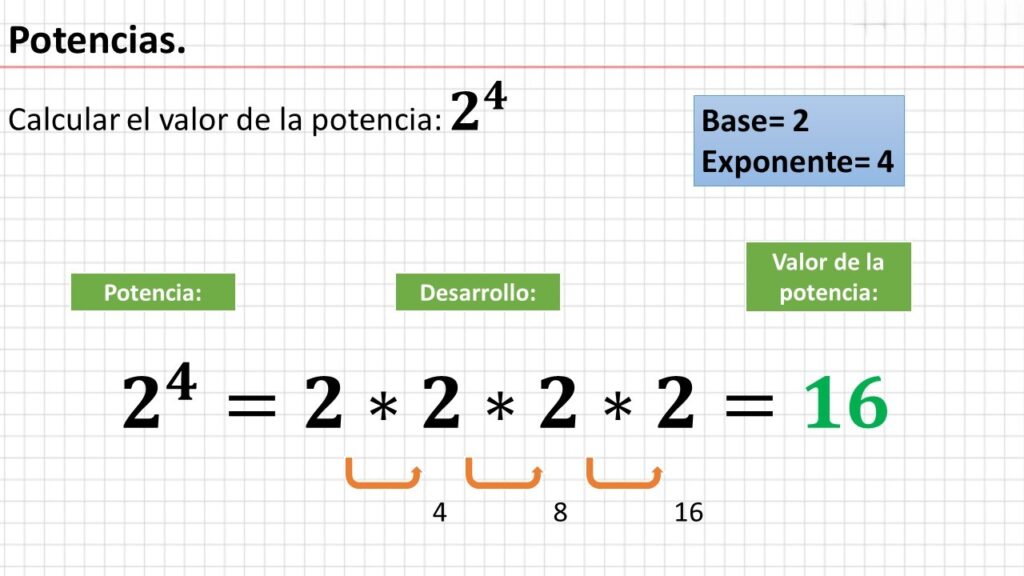
Donde (a) es la base número que se multiplica y (n) es el exponente, número que indica cuántas veces se multiplica la base. Un ejemplo sencillo de potencia es 2⁴, lo que se lee dos elevado a la cuarta potencia y significa 2x2x2x2=16.

Importancia de las potencias en matemáticas

Las potencias tienen una importancia fundamental en matemáticas, con la capacidad para simplificar cálculos complejos. Al expresar relaciones matemáticas de manera compacta y facilitar la resolución de problemas en una amplia variedad de campos.

• Simplificación de cálculos
  • Las potencias permiten representar multiplicaciones repetidas de manera más eficiente, lo que simplifica los cálculos en problemas que involucran grandes cantidades de factores.
• Notación científica
  • Son esenciales para expresar números extremadamente grandes o pequeños en notación científica, comúnmente utilizada en ciencias en física y astronomía.
• Modelos matemáticos y fenómenos naturales
  • Las potencias se utilizan para describir fenómenos que siguen patrones de crecimiento exponencial o decrecimiento.
• Álgebra y ecuaciones
  • Son fundamentales en álgebra avanzada, incluyendo el desarrollo de polinomios, resolución de ecuaciones exponenciales, logarítmicas y en la representación de funciones trascendentes.
• Cálculo diferencial e integral
  • En cálculo, las potencias simplifican el trabajo con derivadas e integrales.
• Tecnología y computación
  • En computación, las potencias son esenciales para el diseño de algoritmos y para expresar la complejidad algorítmica.
• Aplicaciones prácticas
  • Las potencias tienen aplicaciones en múltiples áreas
    • Economía: Cálculo de intereses compuestos.
    • Biología: Modelos de crecimiento exponencial de bacterias.
    • Química: Concentraciones en reacciones químicas.

¿Qué tipos de potencias existen?

Las potencias están formadas de una base y el exponente. La base es el número que se está multiplicando varias veces y el exponente es el número de veces que se multiplica la base. Son una forma compacta de representar una multiplicación repetitiva de un mismo número. Según sus características y aplicación, se pueden clasificar en los siguientes tipos.

• Potencias con exponente positivo
  • Representan una multiplicación repetida del número base.
    • Ejemplo: 2³=2×2×2=8.
  • El exponente indica cuántas veces se multiplica el número base.
• Potencias con exponente cero
  • Cualquier número elevado a la potencia cero, excepto el cero, es igual a 1.
    • Ejemplo: 5⁰=1.
  • Es una propiedad matemática que surge del concepto de división de potencias con la misma base.
• Potencias con exponente negativo
  • Indican el inverso multiplicativo de la potencia con el mismo exponente positivo.
    • Ejemplo: 2−3 = 1/2³ = seria la fracción 1/8
• Potencias con base negativa
  • El signo del resultado depende del exponente:
  • El exponente es par, el resultado es positivo:
    • (−3)⁴ 3x3x3x3=81
  • El exponente es impar, el resultado es negativo:
    • (−3)³ 3x3x3=−27
  • Es importante distinguir esto de bases negativas sin paréntesis
    • −3² donde la potencia solo afecta al número 3, no al signo.

¿Quién inventó esta operación aritmética?

El concepto fundamental de los exponentes tiene su origen en la antigua Grecia, donde Euclides empleó el término “potencia” para indicar cuántas veces un número debía multiplicarse en sí mismo. En el siglo XIV, Nicolás Oresme utilizó números para representar el concepto de potencias. Los babilonios fueron los primeros en usar las potencias y las raíces alrededor del año 3000 a.C.

La introducción de la notación de números elevados para representar exponentes se produjo en el siglo XVII. Hérigone utilizó símbolos y no elevó el exponente. David Hume, en 1636, introdujo el uso de números romanos (III o IX) para indicar exponentes. En 1637, René Descartes se convirtió en la primera persona en emplear exponentes positivos de la manera moderna.

Las potencias son una herramienta matemática esencial que permite simplificar cálculos y representar cantidades de forma compacta, en problemas que involucran multiplicaciones repetitivas. Su comprensión es clave para avanzar en el estudio de las matemáticas y sus aplicaciones en la vida diaria, la ciencia y la tecnología.