En geometría, el perímetro es la suma de las longitudes de los lados de cualquier figura geométrica plana. Se trata de un concepto clave para las matemáticas, que junto con el de área, que le resulta cercano. Es necesario dominar para poder transitar hacia matemáticas más avanzadas en el álgebra y la trigonometría, que permiten la construcción de polígonos.
El concepto aplica tanto para la distancia de la longitud, o para el contorno de las figuras; en el caso de los círculos pasa a llamarse circunferencia. La mitad del perímetro se denomina semiperímetro. Se representa mediante la letra P.
Aplicaciones prácticas del perímetro
El cálculo del perímetro posee numerosas aplicaciones prácticas, para las labores de arquitectura, ingeniería y construcción. Puede usarse para calcular los bordes o la frontera de un espacio o un objeto, un terreno o una construcción.
- Diseño y construcción
- Cercas y delimitaciones:
- Calcular el perímetro es esencial para determinar la cantidad de material necesario para construir cercas, bardas o muros alrededor de un terreno o propiedad.
- Cercas y delimitaciones:
- Planificación de espacios:
- En la arquitectura, el perímetro ayuda a diseñar habitaciones, patios, jardines y otras áreas.
- Ingeniería y manufactura
- Fabricación de productos:
- En la industria, el cálculo del perímetro es clave para determinar la cantidad de material requerido, ejemplo, para moldes, empaques o envolturas.
- Planos técnicos:
- Ayuda a definir los contornos y dimensiones exactas de piezas o estructuras.
- Fabricación de productos:
- Deportes y recreación
- Diseño de pistas y canchas:
- El perímetro se utiliza para trazar campos deportivos, pistas de atletismo o áreas de juego, asegurando medidas reglamentarias.
- Organización de eventos:
- Para delimitar áreas específicas, zonas de espectadores o recorridos en competencias.
- Diseño de pistas y canchas:
- Educación y matemáticas aplicadas
- Problemas de la vida real:
- En el aula, el perímetro se enseña con una herramienta práctica para resolver problemas cotidianos.
- Problemas de la vida real:
- Seguridad y urbanismo
- Control de accesos:
- En urbanismo, calcular el perímetro de parques, estacionamientos o zonas restringidas.
- Infraestructura vial:
- Se utiliza para delinear áreas de estacionamiento, banquetas o carriles específicos.
- Control de accesos:
- Moda y diseño textil
- Corte de patrones:
- En diseño de ropa, calcular el perímetro es crucial para determinar la cantidad de tela necesaria y ajustar los patrones correctamente.
- Corte de patrones:
- Mercadeo y exhibiciones
- Diseño de vitrinas:
- Ayuda a medir y optimizar el espacio disponible para exhibir productos de manera atractiva.
- Eventos comerciales:
- En ferias y exposiciones, el perímetro se utiliza para organizar los stands o áreas de demostración.
- Diseño de vitrinas:
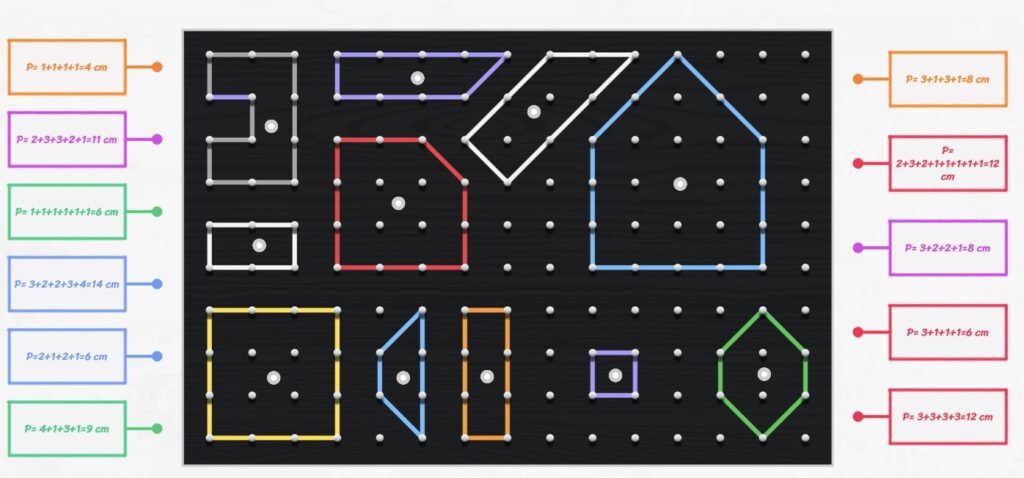
Cálculo del perímetro de figuras geométricas habituales
- Cuadrado
- El cuadrado tiene cuatro lados iguales, x lo que el perímetro se calcula.
- Fórmula: P = 4⋅L
- Donde: L longitud del lado. Ejemplo: El lado mide 5 cm, el perímetro es: P = 4⋅5 = 20 cm
- Fórmula: P = 4⋅L
- El cuadrado tiene cuatro lados iguales, x lo que el perímetro se calcula.
- Rectángulo
- El rectángulo tiene dos pares de lados iguales.
- Fórmula: P = 2⋅(L+A)
- Donde: (𝐿 longitud). (𝐴 ancho). Ejemplo:
- La longitud es 8 cm y el ancho es 3 cm, el perímetro es: P = 2⋅(8 + 3) = 2⋅11 = 22 cm
- Donde: (𝐿 longitud). (𝐴 ancho). Ejemplo:
- Fórmula: P = 2⋅(L+A)
- El rectángulo tiene dos pares de lados iguales.
- Triángulo
- El perímetro se obtiene sumando las longitudes de sus tres lados.
- Fórmula: P = a+b+c
- Donde: a,b,c: longitudes de los lados del triángulo. Ejemplo:
- Los lados miden 5 cm, 7 cm y 10 cm: P = 5 + 7 + 10 = 22 cm
- Donde: a,b,c: longitudes de los lados del triángulo. Ejemplo:
- Fórmula: P = a+b+c
- El perímetro se obtiene sumando las longitudes de sus tres lados.
- Círculo (Circunferencia)
- La circunferencia se calcula con el radio (r) o el diámetro (d):
- Fórmula: P = 2⋅π⋅r o P = π⋅d
- Donde: π\piπ: constante (aproximadamente 3.143.143.14 o 22/7
- Ejemplo: El radio es 7 cm: P = 2⋅3.14⋅7 = 43.96 cm
- Donde: π\piπ: constante (aproximadamente 3.143.143.14 o 22/7
- Fórmula: P = 2⋅π⋅r o P = π⋅d
- La circunferencia se calcula con el radio (r) o el diámetro (d):
- Pentágono regular
- Para polígonos regulares (todos los lados iguales), el perímetro se calcula
- Fórmula: P = n⋅L Donde: (n) número de lados. (L) longitud del lado.
- Ejemplo: Un pentágono tiene lados de 6 cm P = 5⋅6 = 30 cm
- Fórmula: P = n⋅L Donde: (n) número de lados. (L) longitud del lado.
- Para polígonos regulares (todos los lados iguales), el perímetro se calcula
- Polígono irregular
- Para un polígono irregular, simplemente se suman las longitudes de todos sus lados.
- Fórmula: P = suma de todos los lados.
- Ejemplo: Un polígono tiene lados de 4 cm, 5 cm, 7 cm y 6 cm: P = 4+5+7+6 = 22 cm
- Fórmula: P = suma de todos los lados.
- Para un polígono irregular, simplemente se suman las longitudes de todos sus lados.
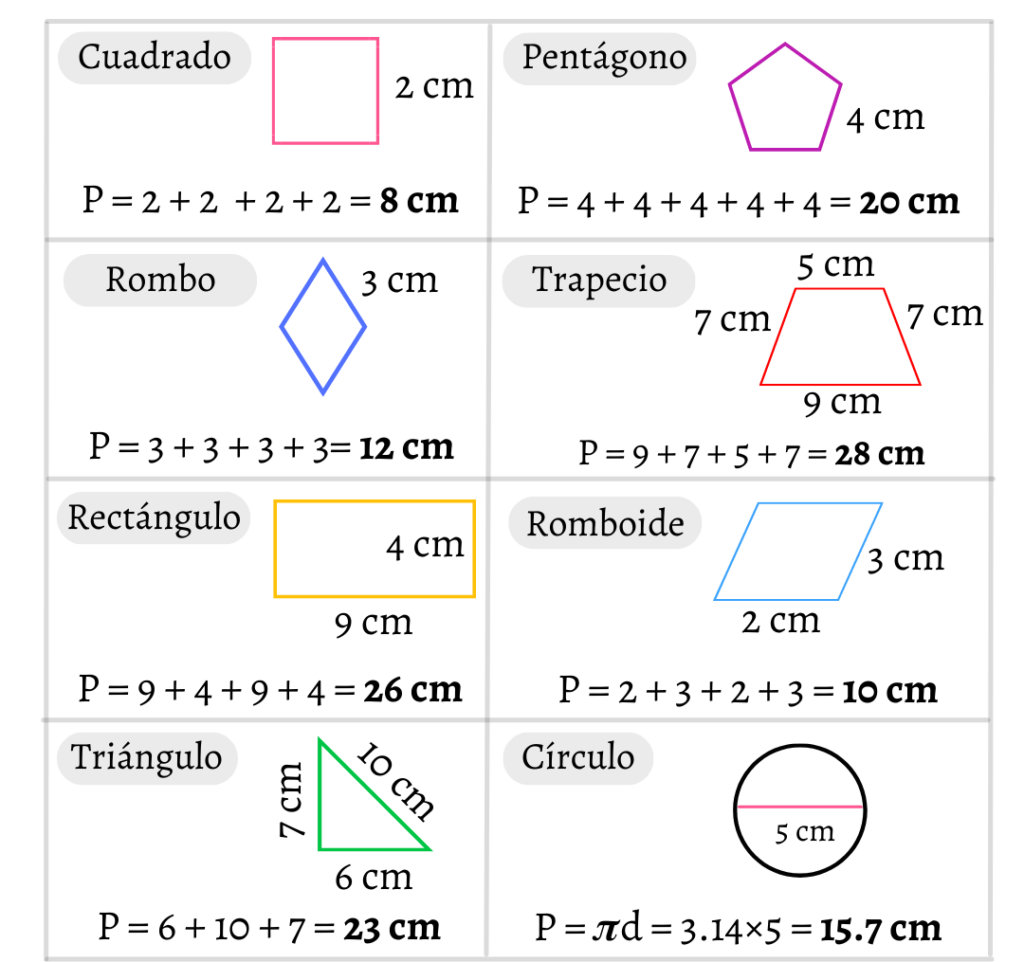
Una medida fundamental en matemáticas
El perímetro es un concepto esencial en geometría que representa la medida total del contorno de una figura plana. En términos simples, es la suma de las longitudes de todos los lados de una figura geométrica. Este concepto es ampliamente utilizado en matemáticas, arquitectura, ingeniería y diversas disciplinas prácticas que requieren medir bordes o límites. El perímetro no solo mide límites, conecta las matemáticas con el mundo real, permitiendo resolver problemas cotidianos de manera práctica y eficiente.
El perímetro es un concepto esencial en matemáticas que nos permite comprender y calcular la medida del contorno de figuras. Sea para construir un jardín, diseñar una cerca o planificar un espacio arquitectónico, el conocimiento del perímetro es útil y aplicable en diversas situaciones cotidianas. Aprender a calcularlo desarrolla habilidades prácticas y fomenta el pensamiento lógico.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?









