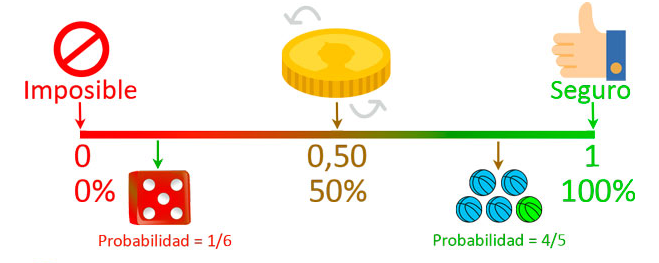
La probabilidad de un evento se debe definir como la medida de la certeza de un suceso dentro de un estudio, investigación o experimento. Para poder llevar a cabo correctamente la teoría de la probabilidad se debe tener presente que los resultados. Invariablemente entran en el rango de la probabilidad de un evento seguro y un evento imposible.
Lo anterior se puede interpretar como que los resultados obtenidos de un experimento en el que se calcula la probabilidad se pueden dividir entre seguros o imposibles. Se le considera a evento seguro o de intervalo abierto, cuando su resultado es de 1 o su equivalente en porcentaje del 100%.
Por otro lago se puede considerar un evento imposible o de intervalo cerrado a aquellos resultados que sean 0 (cero) o su equivalente en porcentaje al 0%. Cualquier resultado que se presente entre estos dos rangos se le considera como un evento intermedio.
El resultado del evento intermedio se representa dependiendo de su posición. En otras palabras, que tan cerca o lejos se ubique del 0 y el 1. Esto quiere decir que entre más cercano sea el resultado a 1, más segura es la posibilidad de que ocurra dicho evento. Por el contrario, entre más cercano este al 0, menor será la probabilidad de que pueda llevarse a cabo.
Clasificación de los Eventos según su Probabilidad
Para simplificar la clasificación de los resultados de los eventos o sucesos, se puede estableces que si la probabilidad de un evento seguro es 1 y de un evento imposible es 0. Sin embargo, se pueden establecer algunas características adicionales, la cuales pueden ayudar a identificarlos de una mejor manera.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea- Evento Seguro.
- Se define como todo aquel evento que SI va a ocurrir CON CERTEZA.
- Su calculo se da cuando el resultado es de 1 (100% en su equivalencia en porcentaje).
- Ejemplo: Si poseemos un dado de 6 caras (1, 2, 3, 4, 5, 6), se puede considerar como un evento seguro que al tirar el dado el número que saldrá será menor o igual a 6.
- Evento Imposible.
- Se puede definir como el resultado de un evento que NUNCA va a ocurrir. En otras palabras, bajo ninguna circunstancia se dará este resultado.
- Su calculo se da cuando el resultado de la probabilidad es igual a 0 (cero).
- Ejemplo: Si tenemos un dado de 6 caras y lo lanzamos al aire podemos asegurar que en ninguna ocasión el resultado va a ser un 7. Esto ya que en un dado NO hay una séptima cara.
Ejemplos de Eventos Seguros e Imposibles
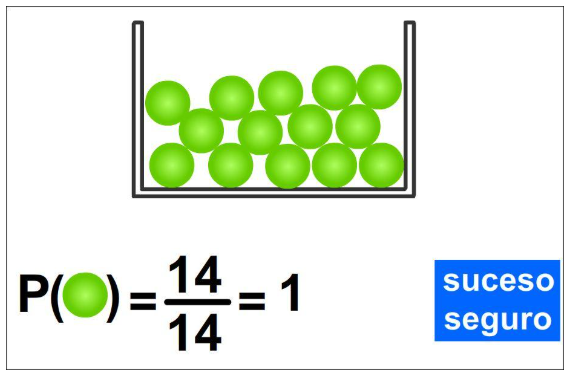
Para poner más claro el concepto sobre el cual la probabilidad de un evento seguro y un evento imposible es 1 y 0. A continuación, se ofrecen varios ejemplos de cada una de las clasificaciones.
- Ejemplos de Eventos Seguros:
- Lanzamiento de una moneda: Al lanzar una moneda al aire, se representa al evento seguro como que el resultado será escudo o corona.
- El Sol: SE puede definir como un evento seguro que todos los días el sol sale por el este.
- Suma de positivos: En el campo de la matemática se puede definir como un evento seguro que al sumar dos números que sean positivos, el resultado siempre será positivo.
- Canicas: Si poseo una bolsa de canicas del mismo color, se puede asegurar como evento seguro que, al sacar una canica de la bolsa, esta será del mismo color que las demás.
- Ejemplos de Eventos Imposibles:
- Número Negativo: Se estima como un evento imposible el obtener un numero Negativo como resultado de la suma de dos números positivos.
- Canicas: Si tenemos una bolsa de canicas donde todas son naranjas, NUNCA podremos obtener una canica verde.

Importancia de la Probabilidad de un Evento Seguro y un Evento Imposible
Al tener bien definido que la probabilidad de un evento seguro es 1 y de un evento imposible es 0. Podemos asegurar que son sin lugar a duda que ellos son los puntos de referencia en cuanto a la teoría de la probabilidad y cada resultado que de ella aparezca será evaluado de acuerdo a estos parámetros.
Ambos conceptos se tornan cruciales para poder definir y comprender el rango completo de cada uno de los posibles resultados de un evento. De esta manera la importancia de la Probabilidad de un Evento Seguro y un Evento Imposible radica en la toma de decisiones con pleno conocimiento de lo que SI o NO va a ocurrir en determinados casos. Esto permite minimizar los riesgos y maximizar la ganancia.









