El plano cartesiano, también conocido como plano de coordenadas es una representación bidimensional, que se compone por dos rectas. Dichas rectas son perpendiculares entre sí, el punto de encuentro de ambas rectas, es conocido como “punto de origen” y su valor corresponde a cero (0, 0).

Las rectas que componen este tipo de plano son conocidas como el eje x (recta horizontal) y eje y (recta vertical). Su función permite localizar la posición de cualquier punto, gracias a las coordenadas dadas por el par ordenado (x, y).  Estas coordenadas son utilizadas para graficar puntos, rectas y algunos otros elementos algebraicos o geométricos.

Estructura de un Plano Cartesiano

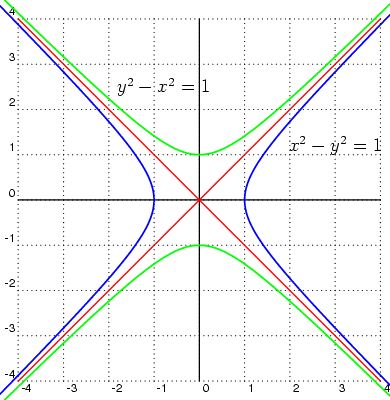
• Punto de Origen: Corresponde al punto en donde se intersecan las rectas perpendiculares del plano de coordinadas. Este punto posee un valor de “0” en ambas rectas.
• Cuadrantes: Las rectas al cruzarse dan paso a la formación de cuatro cuadrantes, en los cuales se divide el plano cartesiano.
  • La identificación de cada cuadrante se hace por medio de números romanos, los cuales corresponde al I, II, III y IV.
  • El orden en que se ubican es en el sentido contrario al reloj. Iniciando desde la zona superior derecha (cuadrante I), posteriormente sigue la zona superior izquierda (cuadrante II), la zona inferior izquierda (cuadrante III) y finalmente la zona inferior derecha (cuadrante IV).
• Ejes: Se les llama de esta manera a las rectas de un plano de coordenadas.
  • Eje x: Corresponde a la recta que se encuentra de forma horizontal, también se le conoce como abscisas.
  • Eje y: Es la recta que se encuentra en una dirección vertical y que es conocida como ordenada.
• Pares Ordenados: Corresponde a la información brindada por el “eje x” y el “eje y”. En su representación primero se da el eje x, seguido del eje y, para después marcar sus posiciones dentro de la gráfica del plano.

Utilización de un Plano de Coordinadas

Para poder utilizar de manera adecuada el plano de coordenadas debe cumplir con ciertos pasos, como los siguientes:

• Ubicación de los puntos o ejes: El objetivo primordial de un plano cartesiano es el de localizar los puntos indicados por la ecuación, problema o función matemática.
  • Cada punto posee una coordenada dentro de los cuatro cuadrantes de la gráfica.
  • Las coordenadas se da por medio de puntos (x, y), los cuales deben ser ubicados y marcados.
  • En algunas ocasiones para obtener. La especificación de los puntos (x, y), es necesario despejar y resolver alguna ecuación, notación, función o problema matemático.
• Gráfica los conceptos: Corresponde a la parte gráfica, la cual se utiliza para localizar de manera visual la ubicación exacta de los puntos (x, y).
  • En la recta vertical o eje x, los números van de los números negativos hasta el punto de origen siguiendo con los números naturas que se ubican de menor a mayor.
  • En la recta horizontal o eje y, los números negativos inician en la parte izquierda hasta llegar al punto de origen, en donde inician los números naturales de menor a mayor.
  • Se debe dibujar la gráfica, mostrando claramente las rectas donde se intersecan, así mismo se debe representar cada cuadrante y su correcta numeración. Lo anterior para que a la hora de marcar la posición de (x, y), esta sea correcta.

La Historia del Plano de Coordenadas

Conocida también por el nombre de Coordenadas Cartesianas, bautizada de esta manera en honor al matemático, filósofo y físico de origen francés René Descartes (1596-1650). Esto debido a su creencia de que todo posee un “punto de partida”.

Descarte, fue el creador de la geometría analítica, e implemento el uso del punto de partida en el sistema Cartesiano. De esta manera se pueda representar a la geometría plana, mientras se usan las dos rectas perpendiculares entre si. Y llamando al punto de unión de estas rectas “Origen de Coordenadas”.

Para el año de 1649, la obra de Descartes sería traducida al latín por Frans Van Shooten. Colaborando de esta manera para el desarrollo del “Sistema de Coordenadas Cartesianas”. La cual sería fundamental durante el desarrollo del “calculo” para pensadores como Gottfried Wilhelm Leibniz o Issac Newton.

Posteriormente el uso del plano de coordenadas se popularizo al desarrollarse el concepto de espacios vectoriales. Con el paso de los años se han realizo nuevos sistemas de coordenadas, las cuales dependen del espacio en donde se utilicen.

• Para el uso de un plano, las “Coordenadas polares” o “Coordenadas esféricas”.
• Para espacios tridimensionales se usan las “coordenadas tridimensionales”.

Importancia del Plano de Coordenadas

Según como se desarrollo el tema, queda claro que los planos de coordenadas pueden facilitar la visualización dentro de la geometría analítica. Ya que vincula al algebre con la geometría mientras localiza puntos de una ecuación, formula o problema en una gráfica.

Es muy útil en áreas como la física, la economía o la estadística ya que facilita el análisis de datos y simplifica la representación de sus movimientos o fluctuaciones. Permitiendo de esta manera comprender los fenómenos complejos gracia a los gráficos.