En el campo de la matemática se puede definir a la probabilidad como un tipo de medida, la cual indica la posibilidad de un evento en ocurrir. Esto quiere decir que una probabilidad es la posibilidad real de que un resultado se de y su frecuencia dentro de una investigación aleatoria. Ya sea el resultado más probable, igualmente probable o menos probable.
Esta medida puede ser definida y explicada de una mejor manera dentro de la Teoría de la Probabilidad, en la cual se estudia dentro de los estudios aleatorios la posibilidad de cada resultado. Actualmente es muy utilizado en campos como la física, la estadística, la economía, las finanzas o la investigación médica.
En cada uno de estos campos se utiliza esta teoría para conocer e investigar más afondo la viabilidad de los sucesos. También se busca entender la mecánica por la cual se dan los diversos resultados dentro de los estudios o investigaciones aleatorias.
Conceptos Clave de la Probabilidad
Para poder poseer una noción más clara sobre esta definición se deben conocer determinados conceptos claves.
- Eventos: Se le conoce de esta manera al con junto de al menos uno o varios resultados que se pueden dar en una investigación aleatoria. Por lo general se clasifican de acuerdo a sus probabilidades.
- Más Posible: Se refiere al resultado con la más alta probabilidad de ocurrir.
- Igualmente Posible: Son aquellos resultados que poseen una igual posibilidad de ocurrir.
- Menos Posible: Define a aquellos resultados que poseen la menor probabilidad de suceder.
- Posibilidad (probabilidad): Es la posibilidad de un resultado de suceder o también se describe como la incertidumbre que se encuentra en un evento.
- Rango: Se refiere al lugar en el que se encuentra un posible resultado, dentro de un determinado porcentaje. Por lo general este va entre el 0% y hasta el 100% de probabilidades de ocurrir.
- Cálculo: Es aquella formula, predicción u operación matemática, que permita establecer claramente cual será el resultado a ocurrir en determinado caso.
- Regla de Laplace: Conocida también como el cálculo teórico. Es aquel que se puede realizar al dividir el número de casos favorables, entre el total de casos posibles. Siempre que en todos los casos el resultado posea posibilidades iguales de ocurrir.
- Frecuencia: Se da cuando se repite el experimento en varias ocasiones y contando cada uno de los resultados que se dan. En otras palabras, contar la frecuencia con la que se da un resultado.

Ejemplos de Fórmulas Aplicaciones
Es normal que para calcular la probabilidad se utilicen dos fórmulas las cuales son:
- Conversión entre formatos: Corresponde al paso de los resultados dados en decimales o fracciones y convertirlos en porcentajes. Ejemplo: Si tenemos una probabilidad del 0,5 (decimal), equivaldría a ½ (fracción) y por tanto seria en porcentaje un 50%.
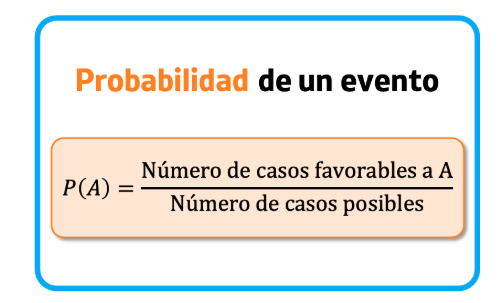
- Probabilidades teóricas: Esta se presenta cuando para lograr la probabilidad de un evento se hace la división entre el número de casos favorables y el número de casos posibles.
Por otra parte, es importante destacar las aplicaciones en las que se llegan a desarrollar las probabilidades en diferentes campos.
- Ciencias: En este campo más científico se suele utilizar para modelar los distintos fenómenos aleatorios que se presentan en la física, química o biología.
- Economía y Finanzas: Dentro de estas especialidades, se suele utilizar las probabilidades de los conjuntos de datos para comprender de una manera más fácil el compendio de información. Adicionalmente con las probabilidades se puede llegara a evaluar la información de los posibles riesgos y ventajas para realizar una toma informada de decisiones.
- Estadística: Más comúnmente usada en esta rama para analizar los resultados, sus datos y poder llegar a predecir los posibles resultados y tendencias del mercado o a fines.
La importancia de la probabilidad

El estudio de la información, así como de los posibles resultados en investigaciones o estudios aleatorios. Son la fuente primordial de las probabilidades de diversos resultados, los cuales se vuelven cruciales. A la hora de tomar una decisión, cuantificar la incertidumbre o realizar predicciones de futuras tendencias o eventos.
La probabilidad brinda el marco para poder evaluar las hipótesis, así como analizar el significado de los resultados arrojados. Para de esta manera comprender los patrones que arrojan los distintos resultados y su aplicación en los distintos campos en los que son aplicados. Los cuales van desde la vida cotidiana, hasta la ciencia, tecnología, matemática y medicina.









