Cuando se habla de una inecuación de primer grado, se refiere a la desigualdad que existe entre dos expresiones algebraicas. Dichas expresiones incluyen una o mas incógnitas y son expresadas generalmente con los signos de < (menor que), ≤ (menor o igual que), > (mayor que) o ≥ (mayor o igual que).
Al resolver la inecuación significa que se deben encontrar todos y cada uno de los valores de la incógnita o variable. Cada uno de los valores de la incógnita son los que hacen que la desigualdad algebraica sea verdadera. La palabra inecuación proviene del latín donde “in” (no) y “aequatio” (igualación).
Ejemplo: 2x < 2 o 3x -2 < 9.
De igual manera que se hace la diferenciación de ecuación e igualdad. Una inecuación de primer grado, que esta sea valida en todas sus variables se le conoce como inecuación incondicional. Por otro lado, si solamente son validas solo para algunos valores de las variables se les llama inecuaciones condicionales.
- Inecuación Incondicional: |x|≤|x|+|y|.
- Inecuación Condicional: -2x + 7 < 2.
Clasificaciones Principales
- Desigualdad: En una inecuación se utilizan los signos de orden <, >, ≤, o ≥, en lugar del signo de igualdad (=) usado en una ecuación.
- Incógnitas: En con junto con los valores conocidos, en las inecuaciones se incluyen valores desconocidos, utilizando las letras en su representación, como por ejemplo la “x”.
- Conjunto de Soluciones: para encontrar la solución a una inecuación se debe al conjunto de valores que satisfagan a la desigualdad y NO a un único valor.
Según los criterios más utilizados en la clasificación de la inecuación de primer grado se puede dar el siguiente ejemplo: x < 0
- Dos incógnitas: x < y.
- Tres incógnitas: x < y + z.
Si tomamos en cuenta la potencia de la incógnita.
- Primer Grado: Se da cuando el exponente mayor de la incógnita de la inecuación es uno. Ejemplo: x+1 < 0.
- Segundo Grado: Llamadas también cuadráticas se dan cuando el mayor exponente de cualquier incógnita es dos. Ejemplo: x²+1 < 0.
- Tercer Grado: Conocida también como Cúbica, en la cual el mayor exponente es tres. Ejemplo: x³ +1 < 0.
Historia de la Inecuación de Primer Grado
Después de la creación de las ecuaciones, irremediablemente surgieron las inecuaciones alrededor de los años 1700 A.C – 1700 D.C en la antigua Grecia. Esto se dio ya que los matemáticos se dedicaban a la exploración de la comparación y relación de los números con variables. Buscando los distintos valores de la variable que puedan cumplir la desigualdad.
Fue hasta que el matemático Diofanto de Alejandría incluyo la incógnita auxiliar para la solución de las ecuaciones cuadráticas o de segundo grado que logro reducir los problemas de las ecuaciones lineales y de las desigualdades.
Con el paso de los años el concepto de la inecuación de primer grado se fue formalizando, en conjunto con los signos (<, >, ≤, o ≥) que representan las desigualdades de dos cantidades. El objetivo principal de su desarrollo se da al resolver, representar o comprender a los problemas que tienen un conjunto de soluciones. Las cuales podrían representarse a través de las desigualdades de una incógnita y una cantidad.
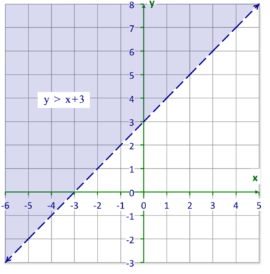
Sistemas de la Inecuación de Primer Grado
En el sistema de la inecuación, puede intervenir al menos dos o más inecuaciones, aún cuando no todos los sistemas poseen solución. Un ejemplo claro de un conjunto o sistema de la inecuación de primer grado es la siguiente:
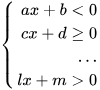
El conjunto de números reales que pueden verificar a la misma vez todas las inecuaciones, se le conoce como la solución del sistema.
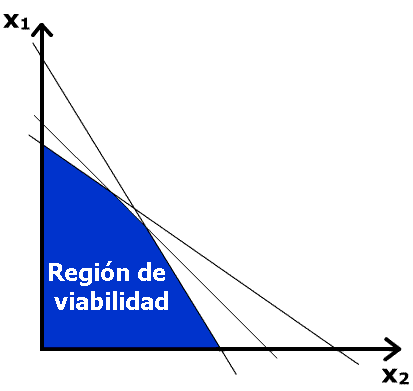
La inecuación de primer grado, permite resolver o modelar algunos problemas dentro de la vida cotidiana. Ejemplos como la reducción de presupuesto, límites de tiempo, análisis de costos o incluso metas de producción. Funcionan como un pilar fundamental en el desarrollo del razonamiento usado en el algebra, además de diversos conceptos matemáticos y en otras áreas como la ingeniería, finanzas o ciencias.
