Para la ubicación en la recta númerica usamos el punto origen o cero y una medida de referencia. Ubicamos el resto de números haciendo otras marcas a la derecha. Para ubicar los enteros seguiremos usando la misma medida de referencia, esta vez haremos las marcas hacia la izquierda del origen.
La ubicacion en la recta numérica está naturalmente dividida en dos mitades idénticas y simétricas respecto al origen con el número cero. Esta recta numérica es una línea en la cual se suelen graficar los números enteros en puntos que están separados, en una distancia uniforme y nos permite localizar, comparar números y realizar operaciones de suma y resta.
Importancia de la ubicación en la recta numérica
La ubicación en la recta numérica es fundamental para comprender la relación y el valor relativo de los números. En la recta numérica es una herramienta visual que ayuda a entender mejor la naturaleza de los números y sus relaciones. Es esencial tanto en la enseñanza y en la aplicación práctica de las matemáticas.
- Visualización de la magnitud de los números:
- La recta numérica permite visualizar cómo los números se relacionan entre sí en términos de magnitud. Es fácil ver que el número 5 es mayor que 2 y está ubicado a la derecha de 2 en la recta.
- Identificación de operaciones matemáticas:
- La recta numérica ayuda a realizar operaciones matemáticas enla suma y la resta. Sumar un número se verá en un desplazamiento hacia la derecha, y restar es un desplazamiento hacia la izquierda.
- Comprensión de los números negativos:
- La recta numérica incluye números negativos a la izquierda del cero, lo que ayuda a los estudiantes a entender que los números negativos son menores que cero y cómo se comportan en operaciones matemáticas.
- Ubicación de fracciones y decimales:
- La recta numérica es una herramienta eficaz para representar fracciones y decimales, lo que facilita la comparación entre ellos.
- Desarrollo del pensamiento abstracto:
- La utilización de la recta numérica fomenta un pensamiento matemático más abstracto y el entendimiento de conceptos la densidad de los números racionales y la relación entre dos números cuales quiera siempre hay un número racional.
- Aplicación en situaciones cotidianas:
- La comprensión de la recta numérica es útil en situaciones del día a día, en la gestión del dinero (deudas y créditos), medir longitudes, temperaturas y más.
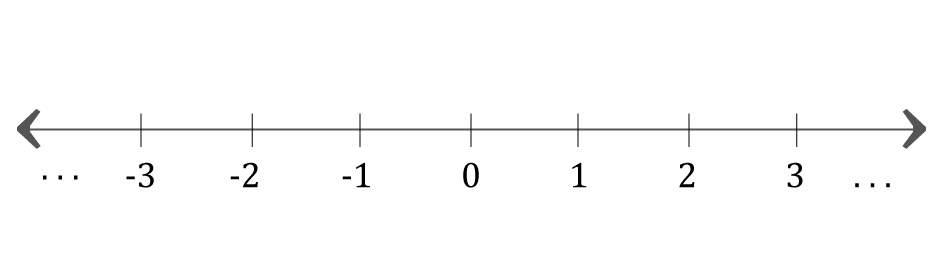
Representar la ubicación en la recta numérica de fracciones
Representamos números racionales en la recta numérica, cada fracción se ubica entre los números enteros, que son las marcas principales de la recta. Los números enteros, -2, -1, 0, 1, 2, etc., representan unidades completas o enteras. Entre estas marcas, se encuentran las fracciones que representan partes de estas unidades.
- Dibuja la recta numérica:
- Traza una línea horizontal y marca puntos equidistantes para los números enteros, 0, 1, 2, -1, etc.
- Identifica la fracción:
- Considera una fracción 𝑎/𝑏, donde (a) es el numerador y (b) es el denominador.
- Divide el intervalo de 0 a 1 en partes iguales:
- El denominador de la fracción es b, divide el intervalo entre 0 y 1 en b partes iguales. Para 2/5 divide el intervalo de 0 a 1 en 5 partes.
- Marca la fracción en la recta:
- A partir del 0, (a es positivo) o a la izquierda (a es negativo). En el ejemplo de 2/5 contarías 2 partes a la derecha del 0. Ese será el punto 2/5
- Repite el proceso para otras fracciones:
- Para fracciones con el mismo denominador, usa las mismas divisiones.
- Simplificación y fracciones equivalentes:
- Recuerda que algunas fracciones pueden ser equivalentes. 2/4 es equivalente a 1/2 ambas estarán en el mismo punto en la recta numérica.
- Ejemplo de Ubicación de Fracciones:
- Para ubicar 3/4en la recta numérica:
- Divide el intervalo entre 0 y 1 en 4 partes iguales.
- A partir de 0, cuenta 3 partes hacia la derecha. El punto resultante es 3/4
- Para ubicar −1/2 en la recta numérica:
- Divide el intervalo entre 0 y -1 en 2 partes iguales.
- A partir de 0, cuenta 1 parte hacia la izquierda. El punto resultante es −1/2
- Para ubicar 3/4en la recta numérica:

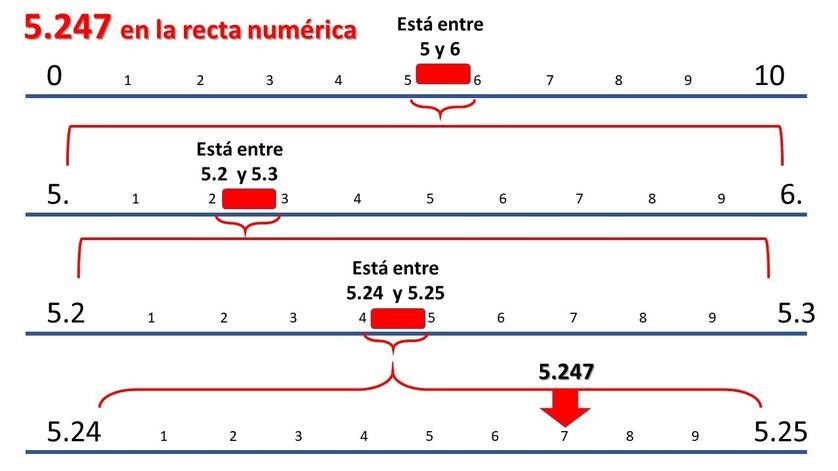
La ubicación en la recta numérica de decimales
En la ubicacion en la recta numérica, los números decimales se representan entre los números enteros. Se divide la sección entre cada número entero en partes iguales, que pueden representar décimas, centésimas o milésimas y su el nivel de precisión necesario. De esta manera, los decimales encuentran su lugar exacto en la recta, permitiendo visualizar con claridad su relación
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea- Pasos para representar la ubicacion en la recta numérica de decimales
- Dibuja una recta numérica:
- Traza una línea horizontal y marca algunos puntos de referencia, 0, 1, 2, 3, etc. Dependiendo del rango de decimales que desees representar.
- Dibuja una recta numérica:
- Divide las secciones entre los números enteros:
- Entre cada número entero, traza divisiones iguales para representar décimas (0.1, 0.2, 0.3, etc.). La décima se divide en centésimas en una representación más precisa (0.01, 0.02, etc.).
- Ubica el decimal en la recta numérica:
- Para ubicar un número decimal 0.6, encuentra el punto entre 0 y 1 y cuenta seis décimas hacia la derecha del 0.
- Ejemplo
- Representar el decimal 1.4 en la recta numérica:
- Se ubica el número entero 1 en la recta.
- Divide la sección entre 1 y 2 en diez partes iguales (décimas).
- 1.4 estará cuatro divisiones a la derecha del 1.
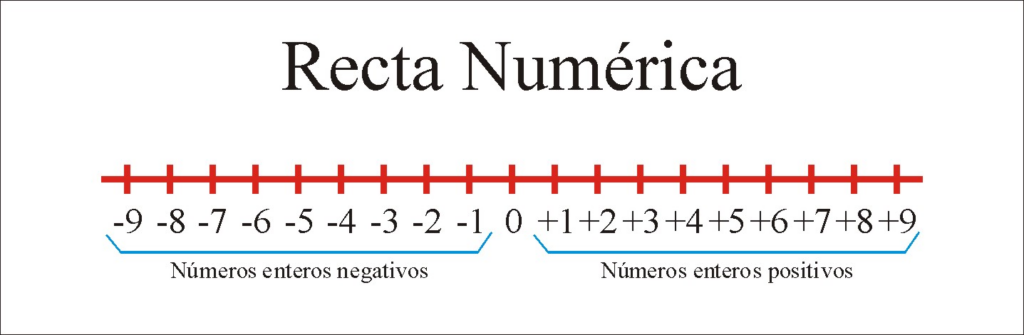
Línea de números negativos y positivos
La sección de la recta numérica situada a la izquierda del cero forma una recta numérica negativa y que la sección situada a la derecha del cero contiene todos los números positivos y forma una recta numérica positiva. Puede extenderse hasta el infinito desde ambos extremos (derecho e izquierdo).
- Ejemplo 1: Línea de números básicos
- Los números negativos (-3, -2, -1) están a la izquierda del 0.
- Los números positivos (1, 2, 3) están a la derecha del 0.
- Ejemplo 2: Línea de números con fracciones y decimales
- Los números negativos incluyen decimales y fracciones -2.5, -1.5, y -0.5.
- Los números positivos incluyen decimales y fracciones 0.5, 1.5, y 2.5.
- Ejemplo 3: Línea de números más extendida
- Los números negativos van desde -5 hasta -1.
- Los números positivos van desde 1 hasta 5.
Un concepto matemático esencial en la vida diaria
La ubicacion en la recta numérica es una herramienta visual y conceptual fundamental en matemáticas, que no solo se limita a las aulas, se encuentra aplicaciones prácticas en la vida diaria. Comprender cómo se ubican los números en esta línea imaginaria puede ayudarnos a interpretar, comparar y resolver situaciones cotidianas de manera efectiva.
La ubicación en la recta numérica es mucho más que un concepto matemático; es una herramienta versátil que nos ayuda a interpretar y gestionar información en nuestra vida cotidiana. Desde la administración de finanzas hasta la planificación del tiempo y la comprensión del entorno que nos rodea, este simple recurso visual nos proporciona una manera clara y efectiva de ver el mundo a través de los números.









