La representación mixta de fracciones se denominan así porque están formadas por un número entero y por una fracción. Hay diversas situaciones donde se usan, unas de ellas son las recetas de cocina, donde se suelen emplear fracciones mixtas para representar cantidades. Por ejemplo “2 ½ de tazas de azúcar” hacen referencia a dos tazas y media de ese ingrediente.
La importancia de la representación mixta de fracciones
Los números mixtos son esenciales en el currículo escolar para enseñar a los estudiantes cómo trabajar con fracciones de manera eficiente. Son un paso intermedio crucial antes de introducir decimales y porcentajes, proporcionando una transición más fluida entre diferentes formas de representación numérica.
- Facilita la Comprensión:
- Visualización: Los números mixtos son más intuitivos y fáciles de visualizar. Por ejemplo, es más sencillo entender 1 ½ como un entero y medio que 3/2.
- Conceptualización: Ayuda a los estudiantes a comprender mejor la relación entre números enteros y fracciones, proporcionando una base sólida para el aprendizaje de conceptos más avanzados en matemáticas.
- Aplicación Práctica:
- Medición y Cocina: En la vida diaria, especialmente en la cocina y en la carpintería, las medidas a menudo se expresan en números mixtos (por ejemplo, 2 ¼ tazas de harina o 3 ½ pulgadas).
- Finanzas: En contextos financieros y comerciales, los números mixtos son comunes, como en la representación de tiempo y dinero.
- Operaciones Matemáticas:
- Problemas de Palabras: En problemas matemáticos, especialmente aquellos basados en situaciones de la vida real, los números mixtos proporcionan una representación más natural y comprensible.
- Simplificación: En ciertos casos, los números mixtos simplifican la solución de problemas al descomponer la fracción en partes más manejables.
- Conexión con Decimales:
- Conversión: Los números mixtos facilitan la conversión a decimales, lo cual es útil en contextos donde se requiere una precisión decimal (por ejemplo, en mediciones científicas).
- Ejemplo Práctico:
- Si un carpintero necesita cortar una pieza de madera de 5 ¾ pies, es más fácil medir 5 pies completos y luego agregar ¾ de pie adicional, en lugar de medir directamente 23/4 pies.
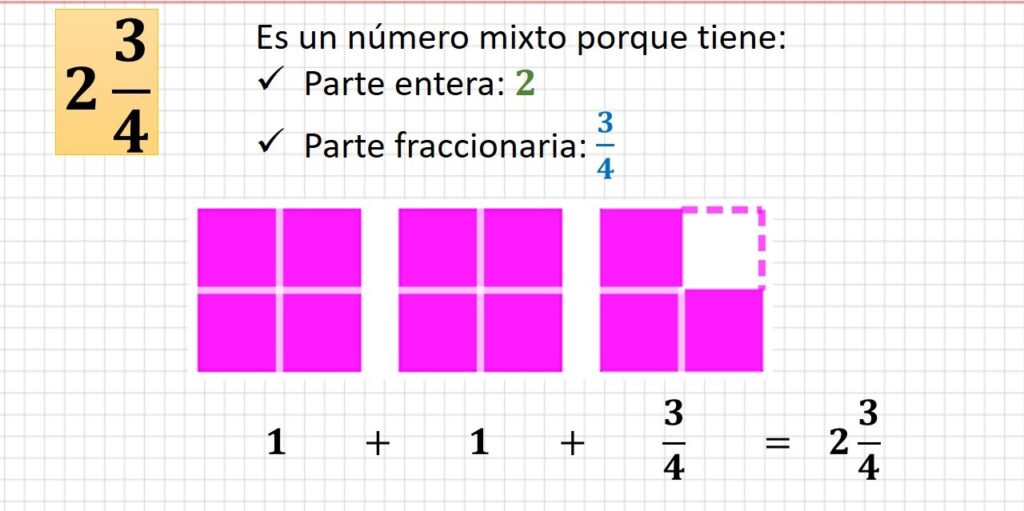
¿Cuál es la representación mixta de fracciones impropias?
La representación de números mixtos o fracciones mixtas son números formados por un número entero (1,2,3,4,5,6,7,8,9..) y una fracción propia (su numerador es menor que su denominador). La representación mixta de fracciones se refiere a expresar una fracción impropia como la suma de un número entero y una fracción propia.
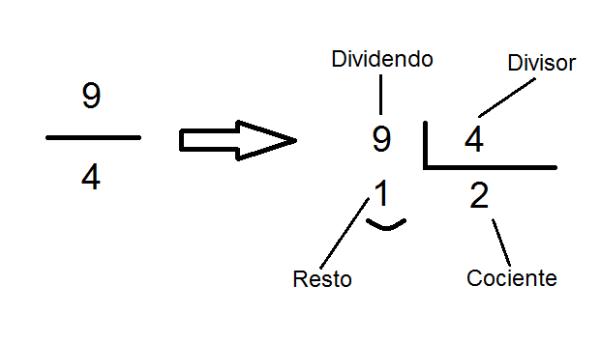
- Proceso de Conversión de fracción impropia a mixta:
- División:
- Fracción Propia:
- La fracción propia se forma con el residuo como numerador y el denominador original permanece igual.
- Ejemplos:
- Convertir 7/4 a fracción mixta. Divide 7 entre 4: el cociente es 1 y el residuo es 3.
- 7÷4=1 (entero) con residuo 3. Fracción mixta es 1 ¾
- Convertir 11/3 a fracción mixta: Divide 11 entre 3: el cociente es 3 y el residuo es 2.
- 11÷3=3 (entero) con residuo 2. Fracción mixta es 3 ⅔
- Dividir el numerador por el denominador para obtener el número entero.
- El residuo se convierte en el numerador de la fracción propia.
- El denominador permanece igual.
- Convertir 7/4 a fracción mixta. Divide 7 entre 4: el cociente es 1 y el residuo es 3.
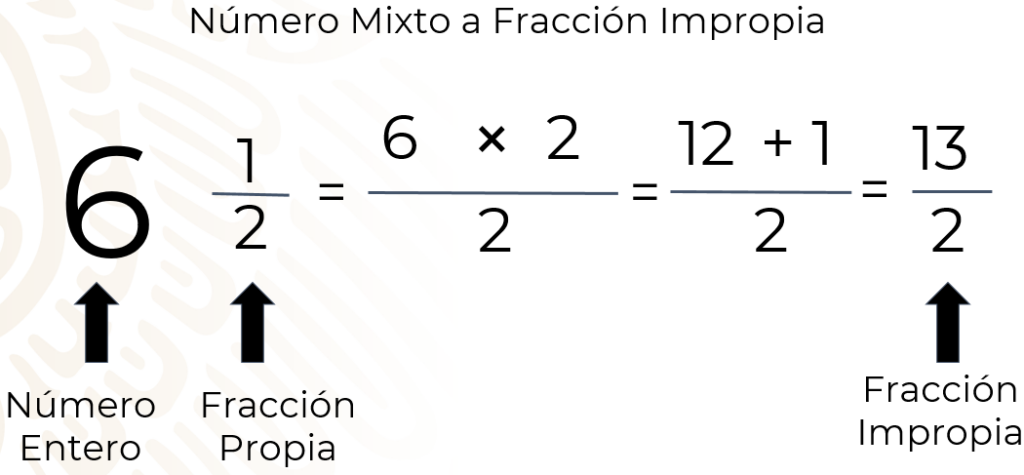
¿Cómo convertir una representación mixta a fracción impropia?
La representación mixta de una fracción nos regala la oportunidad de convertirla en una fracción impropia, multiplicamos el número entero por el denominador y sumamos el numerador. Luego colocamos este resultado sobre el denominador original. Ya que la fracción mixta consta de un número entero y una fracción propia (una fracción donde el numerador es menor que el denominador)
- Conversión de fracción mixta a fracción impropia:
- La fórmula es la siguiente:
- Fracción Mixta = 4 ⅔ ⟹Fracción Impropia 4×3+2 = 14/3
- Ejemplos 1:
- Ejemplo 2:
Facilitando la comprensión de fracciones en matemáticas
La representación mixta de fracciones en matemáticas combina una parte entera y una fracción propia, proporcionando una forma intuitiva de expresar cantidades mayores que uno pero no enteras. Esto es útil para facilitar la comprensión y manipulación de fracciones en contextos cotidianos y educativos.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en líneaPara convertir una fracción impropia a su forma mixta, se divide el numerador por el denominador, obteniendo una parte entera y un residuo. Este residuo se convierte en la nueva fracción, usando el mismo denominador. La representación mixta es especialmente útil en situaciones donde se necesita visualizar o trabajar con fracciones de manera más clara y manejable.
La representación mixta de fracciones no solo simplifica la forma en que entendemos y usamos las fracciones en la vida diaria, sino que también es una herramienta fundamental en la educación matemática. Esto facilita el aprendizaje y la aplicación de conceptos fraccionarios en todo momento. Esta forma intuitiva de expresar cantidades no enteras simplifica la comprensión y manipulación de fracciones, siendo una herramienta valiosa tanto en contextos cotidianos como educativos.









