Las fracciones equivalentes son aquellas que, aunque tengan números diferentes en el numerador y el denominador, representan la misma cantidad o valor. Dos fracciones son equivalentes si al simplificarlas (o multiplicar ambas partes por el mismo número) se obtiene el mismo resultado.

La importancia de las fracciones equivalentes

Las fracciones equivalentes son importantes en matemáticas y en la vida cotidiana. Porque ayudan a entender y comparar cantidades de forma más flexible y a realizar operaciones con fracciones de manera más sencilla. Entender y utilizar estas fracciones ayuda a construir una base sólida en matemáticas y mejora la capacidad de resolver problemas de la vida real.

Algunas de las razones clave para su importancia incluyen:

• Simplificación de cálculos:
  • Al utilizar fracciones equivalentes, podemos simplificar problemas y cálculos, haciendo que las operaciones matemáticas sean más manejables y reduciendo la posibilidad de errores.
• Comparación y comprensión:
  • Las fracciones equivalentes nos permiten comparar fácilmente diferentes fracciones y entender mejor las proporciones, ayudando a desarrollar un sentido más intuitivo de magnitud y fraccionamiento.
• Resolución de problemas en contextos prácticos:
  • En situaciones de la vida cotidiana, como medir ingredientes en una receta o ajustar una cantidad en proporción, las fracciones equivalentes ayudan a adaptar cantidades sin cambiar el resultado final.
• Operaciones avanzadas:
  • Las fracciones equivalentes son fundamentales para realizar operaciones como suma, resta, multiplicación y división de fracciones, ya que facilitan encontrar denominadores comunes y simplificar resultados.
• Habilidades en álgebra:
  • Al trabajar con fracciones equivalentes, se desarrollan habilidades importantes que son útiles en álgebra y otros campos matemáticos, ya que muchas ecuaciones y expresiones algebraicas se simplifican de forma similar.

Numerador y denominador la base de las fracciones

Las fracciones de este tipo aunque tienen diferentes valores en su numerador y denominador, representan la misma cantidad o porción de un todo. Esto significa que, a pesar de que sus números sean distintos, el valor de la fracción no cambia. Para que dos de las mismas son equivalentes, deben dividir el todo en la misma proporción.

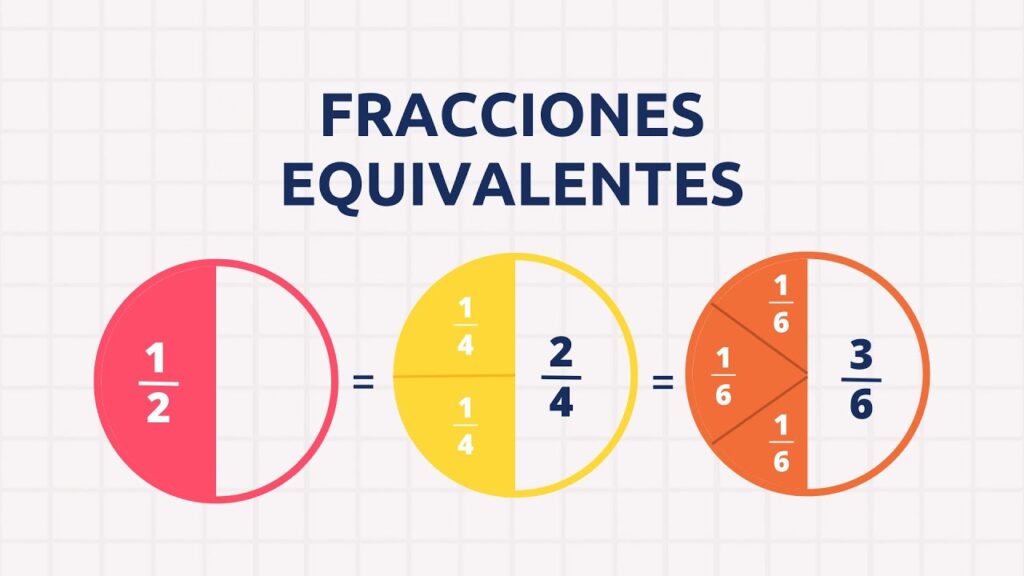
2/1 y 2/4 son equivalentes en ambos casos, representan la mitad de una unidad. Esta equivalencia se logra porque, si multiplicamos o dividimos el numerador y el denominador de una fracción por el mismo número, el valor de la fracción se mantiene igual. La propiedad de equivalencia de estas mismas es fundamental en matemáticas, ya que permite simplificar fracciones o expresar una misma cantidad de formas diferentes.

¿Cómo sabemos son fracciones equivalentes?

Los métodos para determinar si las fracciones equivalentes cumplen de verdad el orden, tienen que incluir lo siguiente productos cruzados, simplificación, decimalización y representación visual. Cada uno tiene sus ventajas y es útil en diferentes contextos. La elección del método depende del tipo de fracción y de las preferencias para la resolución, pero todos ayudan a comprobar la equivalencia de manera eficaz y confiable.

Aquí te explico los dos métodos más comunes:

• Método de productos cruzados:
  • Este método es sencillo y útil cuando tienes dos fracciones, digamos 𝑎/𝑏 y 𝑐/𝑑
    • Para comprobar si son equivalentes:
  • Multiplica el numerador de la primera fracción por el denominador de la segunda (a/d).
  • Luego, multiplica el denominador de la primera fracción por el numerador de la segunda (b/c).
    • Si los productos son iguales, las fracciones son equivalentes.
  • Por ejemplo, para 2/3 y 4/6
    • Producto cruzado: 2×6=12 producto cruzado la otra: 3×4=12
      • Como 12=12, las fracciones son equivalentes
• Simplificación:
  • Otra manera de verificar si dos fracciones son equivalentes es simplificando ambas hasta su forma más simple:
  • Simplifica ambas fracciones dividiendo el numerador y el denominador por su máximo común divisor (MCD).
  • Si al final ambas fracciones tienen la misma forma simplificada, son equivalentes
    • Por ejemplo, si simplificamos 4/6 tenemos: 4÷2= 2 6÷3=3
    • Como ambas fracciones simplificadas son iguales a 2/3 son equivalentes
• Método de Decimales:
  • Otra manera de comprobar la equivalencia de dos fracciones es convertir cada fracción en un número decimal. Si ambas fracciones producen el mismo decimal, son equivalentes. Para hacer esto:
  • Divide el numerador entre el denominador de cada fracción para obtener su forma decimal.
  • Compara los resultados. Si los decimales son iguales, las fracciones son equivalentes.
    • Ejemplo: Supongamos que queremos saber si 1/2 y 3/6
    • Son equivalentes. Dividimos 1÷2=0.5. Dividimos 3÷6=0.5.

Explorando el Universo de las Matemáticas

Las matemáticas son una ciencia fundamental que abarca múltiples áreas de estudio y conceptos, cada uno con aplicaciones prácticas y teóricas esenciales en diversas disciplinas. Desde la aritmética básica, que forma la base de la educación matemática, hasta áreas avanzadas como el cálculo y la estadística, el alcance de esta disciplina es amplio y profundo. El álgebra, con su enfoque en ecuaciones y relaciones abstractas, facilita la resolución de problemas en física, economía y química, mientras que la geometría permite entender y modelar las propiedades del espacio y las formas en arquitectura e ingeniería.

La trigonometría, al estudiar la relación entre ángulos y lados de los triángulos, resulta clave en áreas como la navegación y la astronomía. Por su parte, la estadística y la probabilidad son indispensables para el análisis de datos y la toma de decisiones en campos como la medicina y las ciencias sociales.

Las fracciones equivalentes son fundamentales en el estudio de las fracciones porque permiten simplificar problemas y realizar cálculos de manera más eficiente. Al comprender este concepto, podemos trabajar con fracciones de distintas maneras sin alterar el valor real de la cantidad que representan. Esto no solo es útil en matemáticas, sino que también se aplica en la vida diaria, en situaciones donde se requiere hacer equivalencias, como en la cocina, las finanzas y la construcción.