La fracción propia e propia tiene conceptos importantes que debemos aprender. La fracción propia es aquella donde el numerador es menor que el denominador, lo que implica que su valor es menor que uno. En contraste, una fracción impropia es aquella donde el numerador es igual o mayor que el denominador, lo cual significa que su valor es igual o mayor que uno.
Términos de la fracción propia e impropia
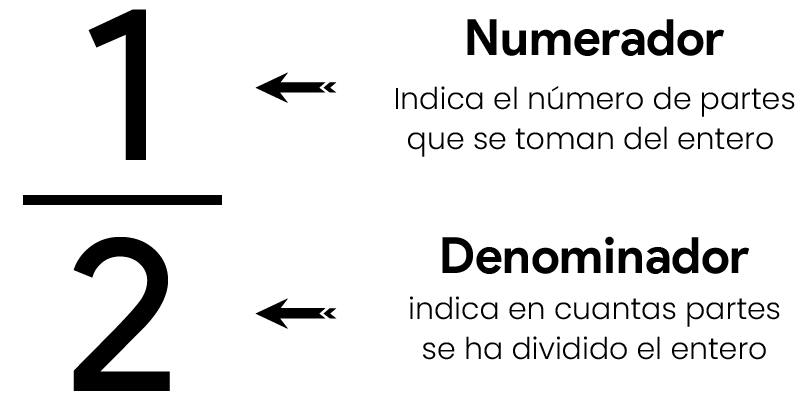
Los términos de una fracción propia e impropia, son el numerador y el denominador. El numerador indica la cantidad de partes que se toman. El denominador señala en cuántas partes iguales se ha dividido la unidad. El numerador es el número que se encuentra en la parte superior de la fracción y representa cuántas partes del todo se están considerando. El denominador, ubicado en la parte inferior de la fracción, indica en cuántas partes iguales se ha dividido el todo.
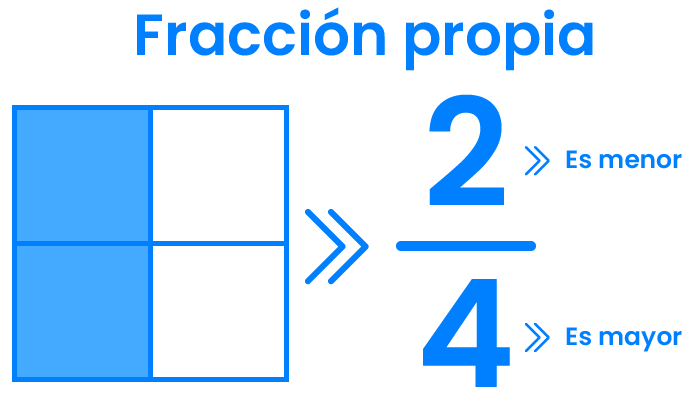
¿Como se representa una fracción propia?
Una fracción propia es una fracción en la que el numerador (el número de arriba) es menor que el denominador (el número de abajo). Esto significa que la fracción representa un valor menor que 1. Esto implica que el valor de la fracción es siempre menor que 1. Matemáticamente una fracción propia representa en (a/b). Vamos haber ejemplos de la diferencia en la fracción propia e impropia.
- Definición de una fracción propia:
- a es el numerador (la parte superior de la fracción),
- b es el denominador (la parte inferior de la fracción),
- a y b son números enteros, a<b (el numerador es menor que el denominador),
- Ejemplos de Fracciones Propias:
- La frscción 1/2 el numerador 1 es menor que el denominador que es 2.
- La fracción 3/4 el numerador 3 es menor que el denominador que es 4.
- La fracción 5/8 el numerador 5 es menor que el denominador que es 8.
- La fracción 7/10 el numerador 7 es menor que el denominador que es 10.
- Conversión de Fracciones Propias:
- Las fracciones propias se pueden convertir en decimales dividiendo el numerador entre el denominador.
- 1/2 es igual a 0.5
- 3/4 es igual a 0.75
- 5/8 es igual a 0.625.
- 7/10 es igual a 0.7
- Las fracciones propias se pueden convertir en decimales dividiendo el numerador entre el denominador.
- Simplificación de Fracciones Propias:
¿Como se representa una fracción impropia?
La fracción impropia se significa que el valor de la misma es mayor o igual a uno. Las fracciones impropias se utilizan a menudo en matemáticas para representar cantidades que superan la unidad completa. Para representar una fracción impropia, se coloca el numerador encima de una línea de fracción y el denominador debajo de dicha línea.
Una fracción impropia puede convertirse en un número mixto, que es una combinación de un número entero y una fracción propia (donde el numerador es menor que el denominador).
- Definición de una fracción impropia:
- a es el numerador (la parte superior de la fracción),
- b es el denominador (la parte inferior de la fracción),
- a y b son números enteros, a>b (el numerador es mayor que el denominador),
- Ejemplos de Fracciones Propias:
- La fracción 5/3 el numerador (5) es mayor que el denominador (3), la fracción impropia.
- Esto cantidad representada es mayor que 1.
- La fracción 8/6 el numerador (8) es mayor que el denominador (6). Esta fracción impropia puede simplificarse 4/3 dividiendo ambos términos entre 2.
- La fracción 11/4 el numerador (11) es mayor que el denominador (4), lo que convierte a la fracción en impropia.
- Suma y Resta:
- Se suman o restan fracciones impropias, debemos encontrar un denominador común y realizar la operación con los numeradores. El resultado es una fracción impropia. Se convertirse a un número mixto para simplificar.
- Multiplicación y División:
- La multiplicación y división de fracciones impropias se realizan de manera similar a las fracciones propias. Se multiplican los numeradores entre sí y los denominadores entre sí. Al dividir se multiplica el recíproco de la segunda fracción.
Importancia la fracción propia e impropia en las matemáticas
Las fracciones propias e impropias son conceptos fundamentales en matemáticas y tienen varias aplicaciones e importancias. Las fracciones propias e impropias son fundamentales en la matemática y la vida diaria, proporcionando una base para la comprensión de conceptos más complejos y aplicaciones prácticas. Su estudio y dominio son cruciales para el desarrollo de habilidades matemáticas y analíticas.
La clasificación de las fracciones en propias e impropias es esencial para comprender y trabajar con ellas de manera efectiva. Las fracciones propias, al tener un numerador menor que el denominador, siempre representan cantidades menores que uno y las fracciones impropias, con un numerador mayor o igual al denominador, representan cantidades iguales o superiores a uno. Entender esta diferencia es crucial para el correcto manejo de fracciones en diversos contextos matemáticos.
