¿Cómo hacemos la división de fracciones?
Esta lección es parte de Temario Matemáticas de Escuela del I y II ciclo Lección 26 de 128Por Andrea del Carmen actualizado el agosto 31, 2026 6 min de lectura 6.144 lecturas
La división de dos fracciones es lo mismo que multiplicar la primera fracción por el recíproco de la segunda fracción. El primer paso para dividir fracciones es encontrar el recíproco (invertir el numerador y el denominador) de la segunda fracción. Después, hay que multiplicar los dos numeradores y por último, los dos denominadores. Finalmente, de ser necesario, se simplifican las fracciones.
Definición
Dividir una fracción entre otra es lo mismo que multiplicar la primera por el recíproco de la segunda. Se le da la vuelta a la fracción que divide (el divisor), se multiplican los numeradores entre sí y los denominadores entre sí, y al final se simplifica si se puede: 5/6 ÷ 2/3 = 5/6 × 3/2 = 15/12 = 5/4.
La relevancia de la división de fracciones#
La división de fracciones es un concepto fundamental en matemáticas que tiene aplicaciones prácticas en la vida cotidiana, en la ciencia y en la tecnología. Entender su importancia facilita el desarrollo de habilidades numéricas y el razonamiento lógico en los estudiantes.
A continuación, se destacan los aspectos clave:
- Utilidad en Situaciones Cotidianas
- La división de fracciones se presenta en muchas situaciones cotidianas, como repartir alimentos o materiales, ajustar recetas, y realizar mediciones precisas.
- Base para Matemáticas Avanzadas
- La división de fracciones sienta las bases para temas de matemáticas avanzadas, como el álgebra, la geometría y el cálculo. Es una herramienta fundamental para simplificar ecuaciones y resolver problemas.
- Desarrollo del Pensamiento Crítico y Lógico
- Este proceso involucra el uso de conceptos como el recíproco, lo cual requiere una comprensión lógica y analítica. Los estudiantes que dominan la división de fracciones desarrollan habilidades de razonamiento que les permiten resolver problemas matemáticos de manera más eficiente y crítica.
- Comprensión de Proporciones y Escalas
- La división de fracciones es esencial en el estudio de proporciones, razones y escalas. En áreas como la ingeniería, la economía y la física, estos conceptos son necesarios para realizar cálculos precisos.
- Competencia en el Uso de Herramientas Tecnológicas
- A pesar de la ayuda de calculadoras, comprender la división de fracciones permite a los estudiantes utilizar estas herramientas de manera más consciente y precisa.
- Fortalecimiento de la Resolución de Problemas Complejos
- La habilidad para dividir fracciones es útil en problemas matemáticos y científicos que requieren varios pasos.
¿Cómo se hace la división de fracciones?#
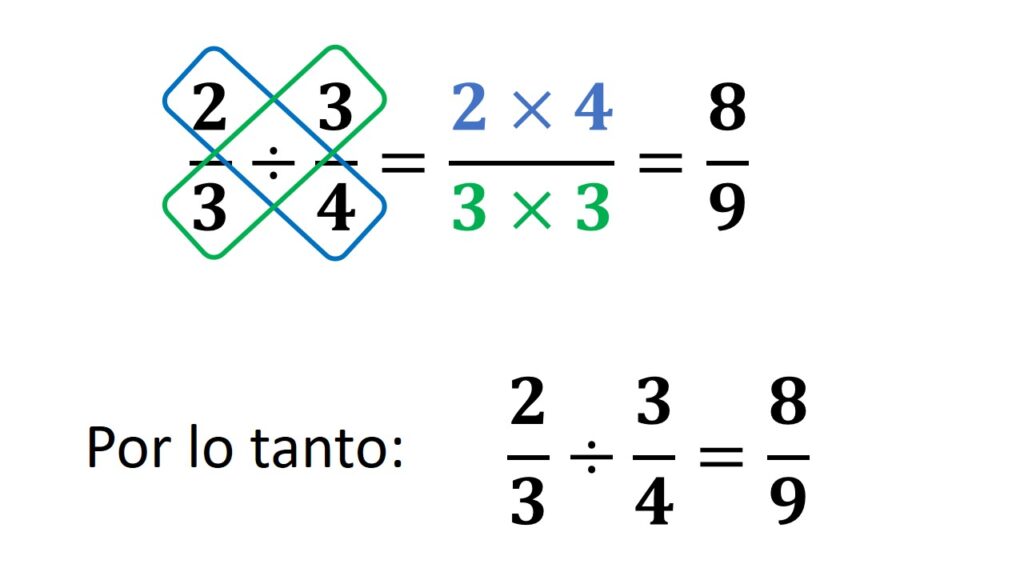
Para la división de fracciones, se invierte la segunda fracción (llamada divisor) y se multiplica por la primera. Luego, multiplicamos numeradores y denominadores respectivamente. El resultado se simplifica si es posible.
Para dividir fracciones, se usa este procedimiento:
- Identifica las fracciones que vas a dividir:
- En una división de fracciones, tienes dos fracciones: la primera es el dividendo y la segunda es el divisor.
- Invierte la segunda fracción (el divisor):
- Esto significa intercambiar el numerador y el denominador de esta fracción.
- Multiplica las fracciones:
- Una vez que tienes el recíproco de la segunda fracción, multiplica la primera fracción por este recíproco. Para multiplicar, simplemente multiplica los numeradores entre sí y los denominadores entre sí.
- Simplifica la fracción resultante, si es posible:
- Esto implica reducir la fracción a su forma más simple dividiendo el numerador y el denominador por su máximo común divisor.
- Ejemplo 1 Si quieres dividir 5/6 ÷ 2/3
- Invertimos la segunda fracción: 3/2
- Multiplicamos: 5×3=15 y 6×2 =12 resultado15/12
- Simplificamos 15÷3=5 y 12÷3=4 resultado final 5/4
- Multiplicamos: 5×3=15 y 6×2 =12 resultado15/12
- Invertimos la segunda fracción: 3/2
- Ejemplo 2 Si quieres dividir 7/8 ÷1/4
- Invertimos la segunda fracción: 4/1
- Multiplicamos: 7×4=28 y 8×1=8 resultado 28/8
- Simplificamos: 28÷4=7 y 8÷4=2 resultado final 7/2
- Multiplicamos: 7×4=28 y 8×1=8 resultado 28/8
- Invertimos la segunda fracción: 4/1
- Ejemplo 3 Si quieres dividir 9/10 ÷ 3/5
- Invertimos la segunda fracción: 5/3
- Multiplicamos: 9×5=45 y 10×3=30 resultado 45/30
- Simplificamos: 45÷15=3 y 30÷15=2 resultado final 3/2
- Multiplicamos: 9×5=45 y 10×3=30 resultado 45/30
- Invertimos la segunda fracción: 5/3
Un viaje por el mundo de las fracciones#
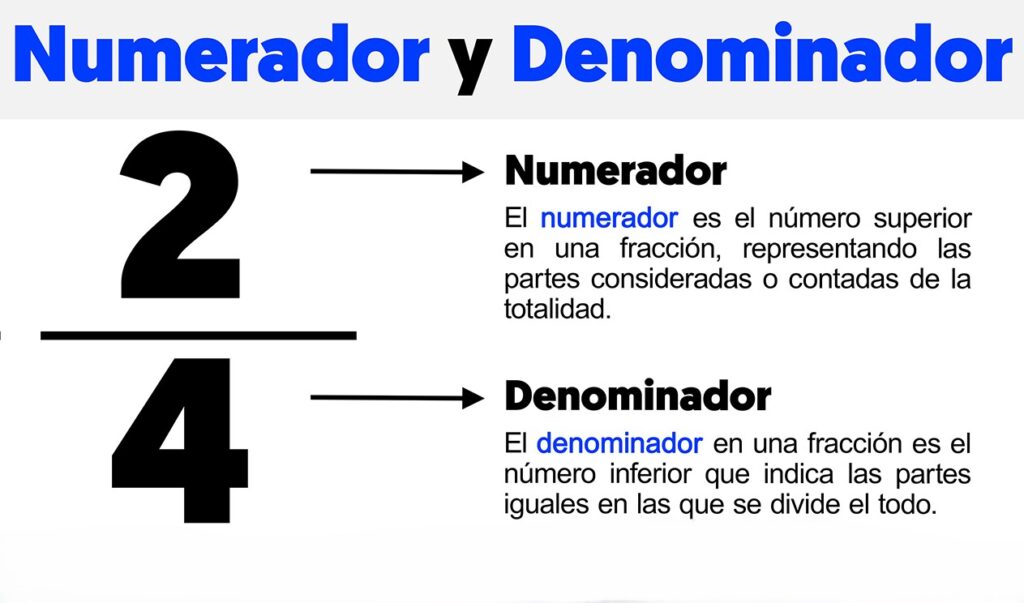
Las fracciones son una de las herramientas matemáticas más antiguas y esenciales, utilizadas para dividir el todo en partes comprensibles. A pesar de su simplicidad aparente, las fracciones abren un mundo de posibilidades en el aprendizaje de las matemáticas. En su forma más básica, una fracción representa una parte de un entero o un grupo de elementos. Si pensamos en un pastel dividido en ocho porciones, una fracción como 3/8 simboliza tres de esas porciones.
El mundo de las fracciones se expande al comprender sus diferentes tipos y aplicaciones. Existen fracciones propias, impropias y mixtas, cada una con características particulares que enriquecen nuestro entendimiento matemático. Además, aprender a sumar, restar, multiplicar y dividir fracciones nos permite resolver problemas complejos de manera lógica y estructurada.
El dominio de la división de fracciones no solo fortalece las habilidades matemáticas, sino que también fomenta el razonamiento lógico y la capacidad de resolución de problemas. Estudiar la división de fracciones no es solo aprender un conjunto de pasos, sino desarrollar habilidades útiles para situaciones cotidianas. Practicar estos procedimientos ayuda a afianzar conceptos matemáticos que serán útiles en estudios avanzados y en la vida diaria.
Ponte a prueba#
¿Cuáles son los pasos para dividir dos fracciones?#
Son cuatro. 1) Identificar las dos fracciones: la primera es el dividendo y la segunda, el divisor. 2) Invertir el divisor, es decir, hallar su recíproco. 3) Multiplicar: numerador por numerador y denominador por denominador. 4) Simplificar el resultado si se puede. Con 5/6 ÷ 2/3: se invierte 2/3 y queda 3/2; se multiplica 5 × 3 = 15 y 6 × 2 = 12, o sea 15/12; y se simplifica dividiendo entre 3, con lo que el resultado final es 5/4.
¿Cuánto es 7/8 ÷ 1/4?#
El recíproco de 1/4 es 4/1, así que la división se convierte en 7/8 × 4/1. Multiplicando: 7 × 4 = 28 y 8 × 1 = 8, o sea 28/8. Como 28 y 8 se dividen los dos entre 4, la fracción se simplifica a 7/2, que es 3,5. Se puede comprobar de otra forma: 7/8 vale 0,875 y 0,875 ÷ 0,25 = 3,5.
¿Qué es el recíproco de una fracción?#
Es la fracción que se obtiene al intercambiar el numerador y el denominador: el recíproco de 3/4 es 4/3, y el de 1/4 es 4/1, que es simplemente 4. Su propiedad clave es que una fracción multiplicada por su recíproco da 1: 3/4 × 4/3 = 12/12 = 1. Por eso multiplicar por el recíproco deshace la división.
¿Por qué al dividir 9/10 entre 3/5 sale un número mayor que 9/10?#
Porque dividir entre una fracción menor que 1 es preguntar cuántas veces cabe esa fracción pequeña en la otra, y cabe más de una vez. Al resolver: 9/10 ÷ 3/5 = 9/10 × 5/3 = 45/30 = 3/2, es decir 1,5. Y es coherente: 3/5 son 0,6, que caben una vez y media en 0,9.
También en matemáticas
